An annular disc is a flat circular ordinary disc, which has a concentric circular hole in it.
(i) Moment of inertia of an annular ring or disc through its centre and perpendicular to its plane:
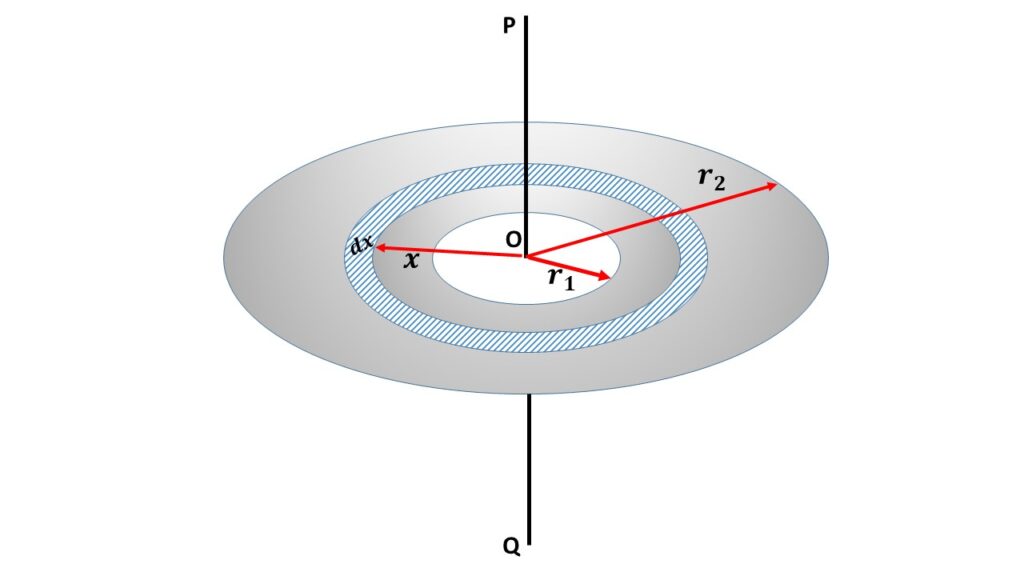
Let us consider an annular ring or disc of inner radius \( r_1 \) and outer radius \( r_2 \), rotating about an axis PQ through its centre O and perpendicular to its plane. Let M be the mass of this disc, so the mass density of the disc is \( \displaystyle{\frac{M}{\pi{(r_2^2-r_1^2)}}} \). Where, \( \pi{(r_2^2-r_1^2)} \) is the area of the disc.
Let us consider a concentric elementary ring of radius \( x \) and thickness \( dx \). So the area of the elementary ring is \( 2\pi{x}dx \) and the mass of the elementary ring is \( \frac{M}{\pi{(r_2^2-r_1^2)}}\times{2\pi{x}dx} \) = \( \frac{2M}{{(r_2^2-r_1^2)}}xdx \)
So the moment of inertia of this elementary ring about the axis PQ is
\( \frac{2M}{(r_2^2-r_1^2)}xdx\cdot{x^2}\\=\frac{2M}{(r_2^2-r_1^2)}x^3{dx} \)
So the moment of inertia of whole annular disc or ring is given by,
\( I_0=\int_{r_1}^{r_2}{\frac{2M}{(r_2^2-r_1^2)}x^3{dx}}\\=\frac{2M}{(r_2^2-r_1^2)}\int_{r_1}^{r_2}{x^3{dx}}\\=\frac{M}{2(r_2^2-r_1^2)}(r_2^4-r_1^4)\\=\frac{1}{2}M{(r_1^2+r_2^2)} \)
CASE-I :
If there is no whole in the disc then \( r_1=0 \) and \( r_2=r \) (say). So the annular ring becomes a plane disc. So then the moment of inertia of this disc is \( I_0=\frac{1}{2}Mr^2 \)
CASE-II :
If the annular disc becomes a circular ring of radius r (say), this means that \( r_1=r_2=r \), then the moment of inertia of the circular ring is \( I_0=Mr^2 \)
Moment of inertia of an annular ring about a diameter:
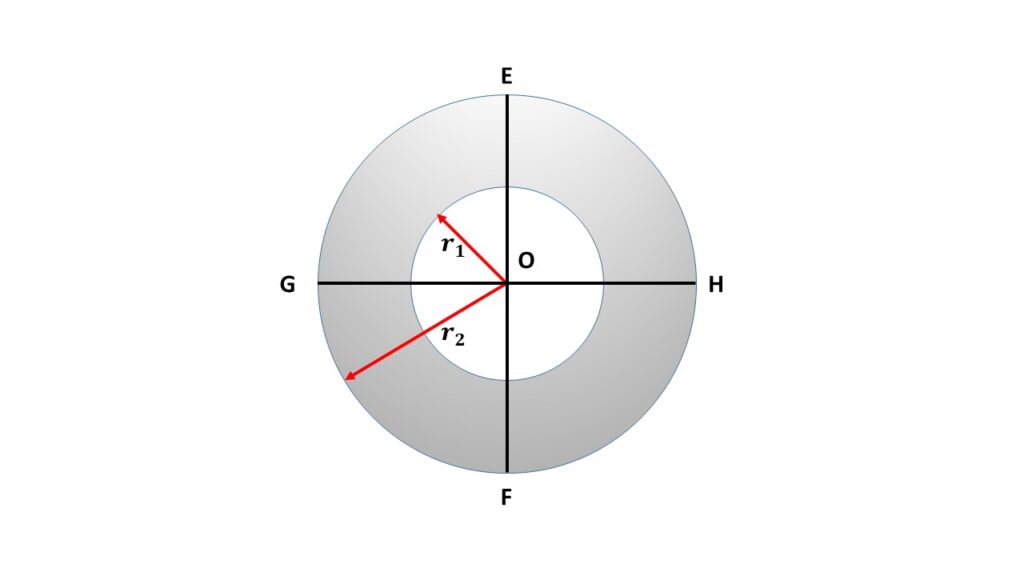
The moments of inertia of the annular disc about any two mutually perpendicular diameters are the same because the annular ring or disc is symmetrical in shape. Let us consider \( I_d \) be the moment of inertia of the annular disc about each of the two mutually perpendicular diameters EF and GH. So by using the theorem of perpendicular axes, we can write the sum of moments of inertia of the annular disc about the diameters EF and GH is equal to the moment of inertia of the annular disc about an axis through the centre O and perpendicular to its plane, this means that
\( I_d+I_d=I_0\\or,\ I_d=\frac{1}{2}I_0 \)
\( or,\ \displaystyle{I_d=\frac{1}{4}M(r_1^2+r_2^2)} \)
CASE-I :
If there is no hole in the annular disc then \( r_1=0 \) and \( r_2=r \) (say), so the moment on inertia of the annular disc about the diameter is \( \displaystyle{I_d=\frac{1}{4}Mr^2} \)
Moment of inertia of an annular disc about a tangent in its own plane:
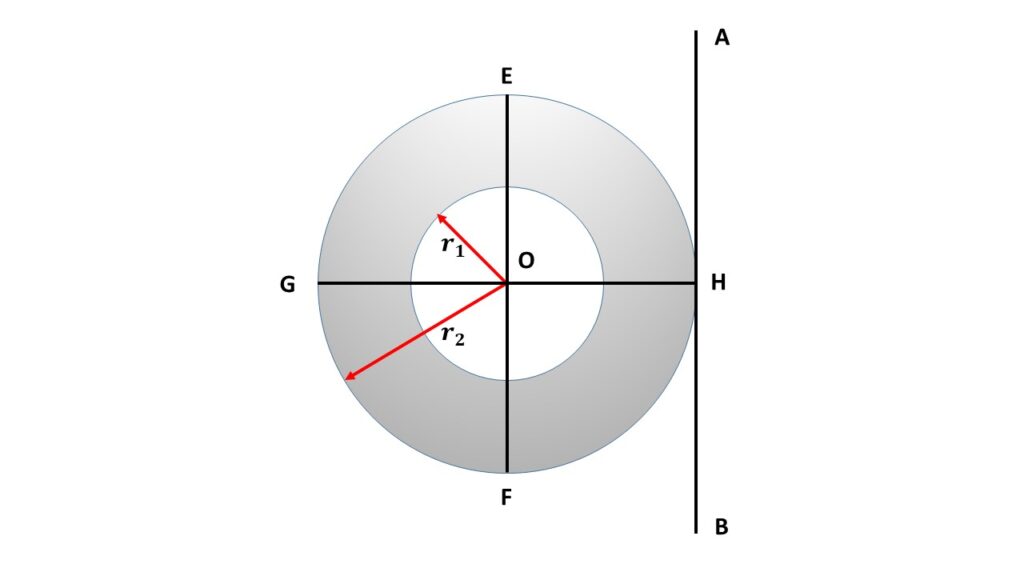
The annular disc or ring is rotating about a tangent AB in its own plane which is parallel to the diameter EF, The perpendicular distance between AB and EF is \( r_2 \), which is the outer radius of the annular ring. Let, \( I_{AB} \) be the moment of inertia of the annular ring about the axis AB.
By using the theorem of parallel axes we can write,
\( I_{AB}=I_d +Mr_2^2\\=\frac{1}{4}M(r_1^2+r_2^2)+Mr_2^2 \)
\( \displaystyle{or,\ I_{AB}=\frac{1}{4}M(5r_2^2+r_1^2)} \)
Moment of inertia of an annular disc or ring about a tangent perpendicular its own plane:
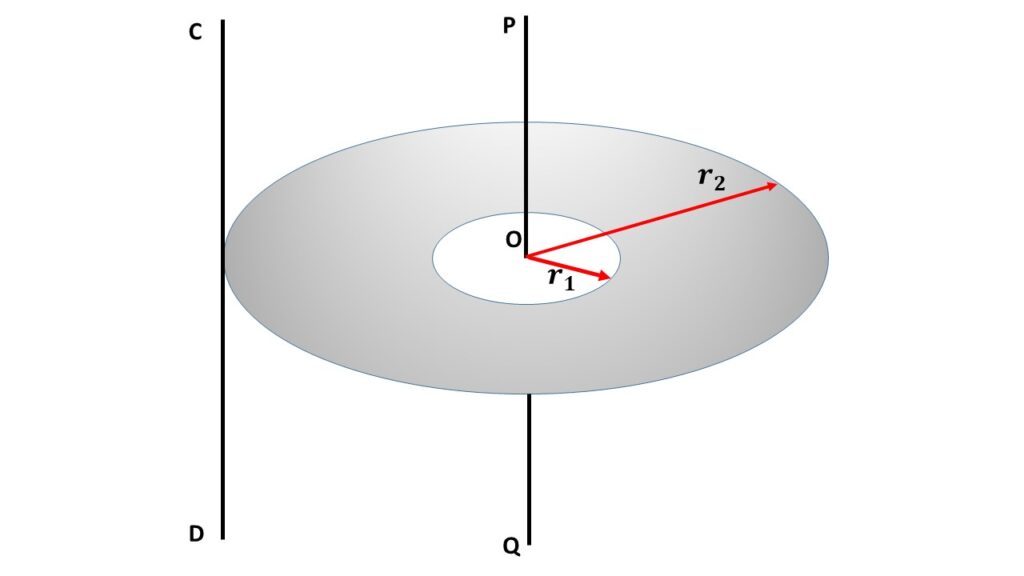
The annular disc or ring is rotating about an axis CD which is parallel to the axis PQ through the centre O of the disc and perpendicular to its plane. So CD is also perpendicular to the plane of the disc. Now the perpendicular distance between PQ and CD is \( r_2 \) which is the outer radius of the ring. By using the theorem of parallel axes, we can write
\( I_{CD}=I_0+Mr_2^2\\=\frac{1}{2}M(r_1^2+r_2^2)+Mr_2^2 \)
\( \displaystyle{or,\ I_{CD}=\frac{1}{2}M(r_1^2+3r_2^2)} \)
CASE-I :
If there is no whole in the disc then \( r_1=0 \) and \( r_2=r \) (say). So the annular ring becomes a plane disc. So then the moment of inertia of this disc is \( I_{CD}=\frac{3}{2}Mr^2 \).
CASE-II :
If the annular disc becomes a circular ring of radius r (say), this means that \( r_1=r_2=r \), then the moment of inertia of the circular ring is \( I_{CD}=Mr^2 \)