(i) Moment of inertia of a plane circular disc about an axis through its centre and perpendicular to its plane:

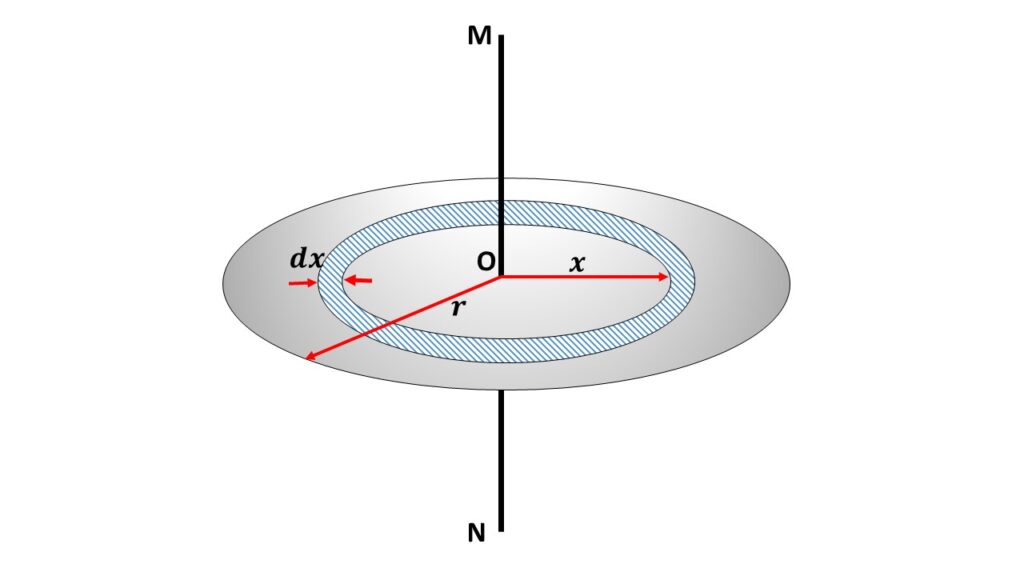
Let us consider a circular disc of radius r and mass M, rotating about a fixed axis MN, which passes through its centre O at a right angle to the plane of the disc. Now the mass per unit area \( \sigma=\frac{M}{\pi{r^2}} \), where \( \pi{r^2} \) is the area of the disc.

Let us consider a circular strip of radius \( x \) and thickness \( dx \) with centre at \( O \). So the area of the circular strip is \( 2\pi{x}dx \) and its mass is \( 2\pi{xdx}\times\frac{M}{\pi{r^2}}=\frac{2M}{r^2}x{dx} \).
The moment of inertia of the circular strip about the axis MN passing through the centre O and perpendicular to the plane of the disc is,

\( \frac{2M}{r^2}x{dx}\cdot{x^2}\\=\frac{2M}{r^2}x^3{dx} \)

So the moment of inertia of the whole disc about the axis MN is given by,
\( I_O=\displaystyle{\frac{2M}{r^2}\int_0^r{x^3}{dx}}\\=\displaystyle{\frac{2M}{r^2}\frac{1}{4}{[x^4]}_0^r}\\=\frac{M}{2r^2}r^4\\=\frac{1}{2}Mr^2 \)

\( \displaystyle{I_O=\frac{1}{2}Mr^2} \)

(ii) Moment of inertia of a plane circular disc about a diameter:

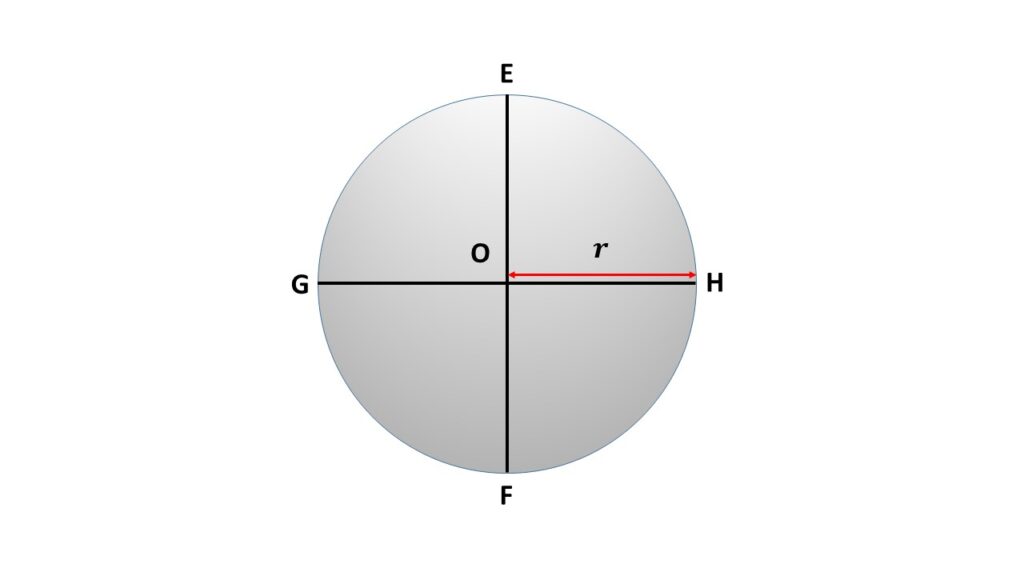
Let us consider two mutually perpendicular diameters EF and GH of the circular disc. Since the disc is symmetrical in shape, so the moments of inertia about the diameters EF and GH are the same which is \( I_d \) (say).

So by using the theorem of perpendicular axes for a laminar body, we can write
\( I_d+I_d=I_O \)
or, \( I_d=\frac{1}{2}I_O \)
or, \( \displaystyle{I_d=\frac{1}{4}Mr^2} \)

Where \( I_0=\frac{1}{2}Mr^2 \), is the moment of inertia of the circular disc about the axis through its centre and perpendicular to its plane.

(iii) Moment of inertia of the circular disc about a tangent:

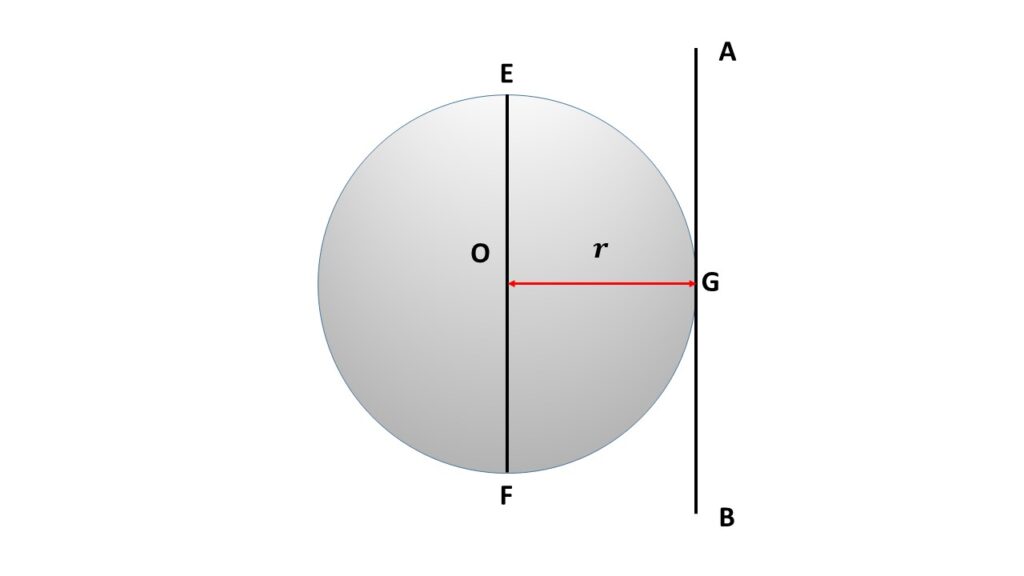
Let, the plane circular disc be rotating about a tangent AB. This is parallel to the diameter EF of the disc. The perpendicular distance between EF and AB is \( r \), which is the diameter of the circular disc.

So by using the theorem of parallel axes, we can write
\( I_T=I_d+Mr^2 \)
or, \( I_T=\frac{1}{4}Mr^2+Mr^2 \)
or, \( \displaystyle{I_T=\frac{5}{4}Mr^2} \)

(iv) Moment of inertia of a place circular disc about an axis tangential to the disc and perpendicular to its plane:

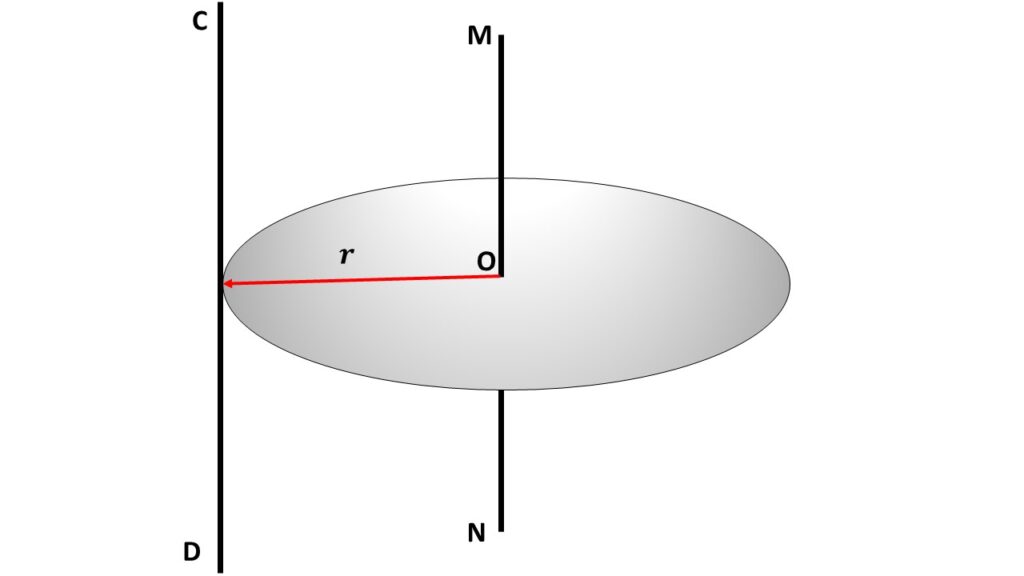
Let us consider an axis CD, which is parallel to the axis MN. The perpendicular distance between these two axes is \( r \), which is radius of the place circular disc.
Now, by using the parallel axes theorem, we can write

\( I_{CD}=I_O+Mr^2\\or,\ I_{CD}=\frac{1}{2}Mr^2+Mr^2\\or,\ I_{CD}=\frac{3}{2}Mr^2 \)

where, \( I_O=\frac{1}{2}Mr^2 \) is the moment of inertia of the circular plane disc about the axis MN, which passes through the centre of the disc.