Couple or torque required to twist a uniform solid cylinder:
Let us consider a uniform solid cylindrical rod of radius \( r \), length \( l \) made of a material of rigidity modulus \( \eta \), this cylindrical rod is clamped at one end and a twisting couple \( \Gamma \) is applied to the lower end in a plane perpendicular to its length with its axis coinciding with that of the cylinder. Due to the shearing strain produced in the rod, shearing stress will be set up within it which will give rise to the restoring couple, whose axis also coincides with the axis of the cylinder.
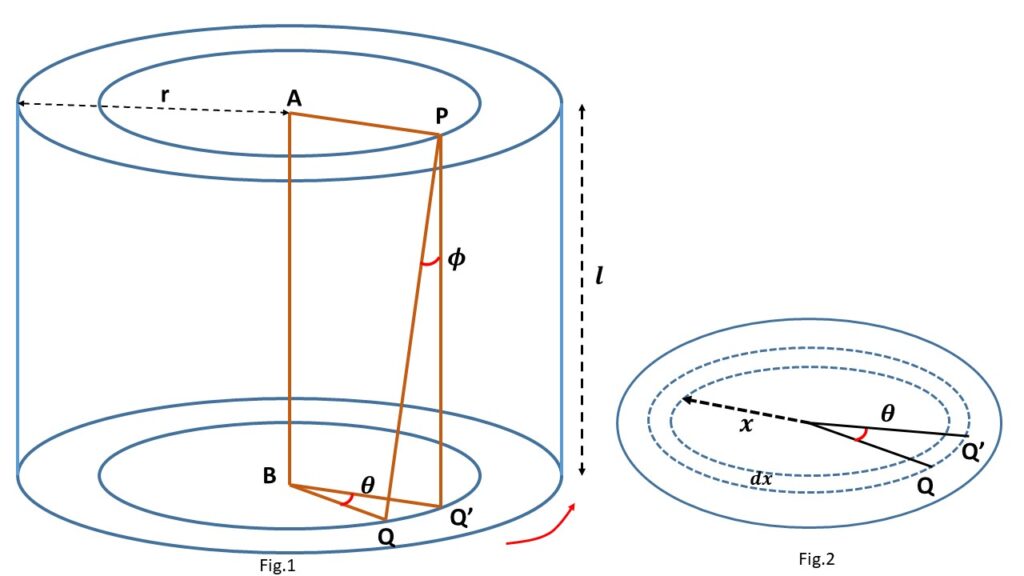
Let us consider, \( \theta \) be the angle of twist at a distance \( l \) from the fixed end which is proportional to both \( l \) and \( \Gamma \). Each radius of the lower end of the cylinder is turned through the same angle \( \theta \), but the displacement is maximum at the rim. This displacement decreases towards the centre. At the centre the displacement is zero. Now let us consider a ring of radius \( x \) and thickness \( dx \) in the lower end of the rod, as shown in Fig.2. Now a point on the ring \( Q \) is displaced to the point \( Q’ \) through an angle \( \theta \). So the linear displacement is given by, \( QQ’=x\theta=l\phi \) or, \( \displaystyle{\phi=\frac{x\theta}{l}} \). Where \( \phi \) is the angle of shear. This angle of shear is maximum at the rim and zero at the axis of the cylinder.
We know that the modulus of rigidity \( \eta=\frac{shearing\ stress}{shearing\ strain}=\frac{T}{\phi} \).
or, \( T=\eta\phi=\eta\cdot\frac{x\theta}{l} \)
where \( T \) is the shearing stress.
The cross section area of the ring of radius \( x \) and thickness \( dx \) is \( 2\pi{x}dx \).
Therefore the shearing force on the ring is \( F=T\times{2\pi}xdx=\frac{2\pi\eta\theta{x^2}}{l}dx \).
Now the torque about the axis of the cylinder is given by,
\( \frac{2\pi\eta\theta{x^2}}{l}dx\cdot{x}=\frac{2\pi\eta\theta}{l}\cdot{x^3}dx \)So the total torque on the cylinder is
\( \displaystyle{\Gamma=\frac{2\pi\eta\theta}{l}\int_0^r{x^3}dx\\=\frac{2\pi\eta\theta}{l}\frac{r^4}{4}} \)or, \( \displaystyle{\Gamma=\frac{\pi\eta{r^4}}{2l}\theta} \)
Now the twisting couple per unit twist is,
\( \displaystyle{\tau=\frac{\Gamma}{\theta}=\frac{\pi\eta{r^4}}{2l}} \)This is known as the torsional rigidity of the material of the cylindrical rod.