Moment of inertia about an arbitrary axis:

Let us consider, three mutually perpendicular axes OX, OY and OZ meeting at the origin O. Now we want to calculate the moment of inertia of a body about any axis ON, passing through the origin O.

Let us consider, \( m_i \) be the mass of the \( ith \) particle of the body, and \( \vec{r}_i \) be the position vector of the ith particle at the point P with respect to the origin O.

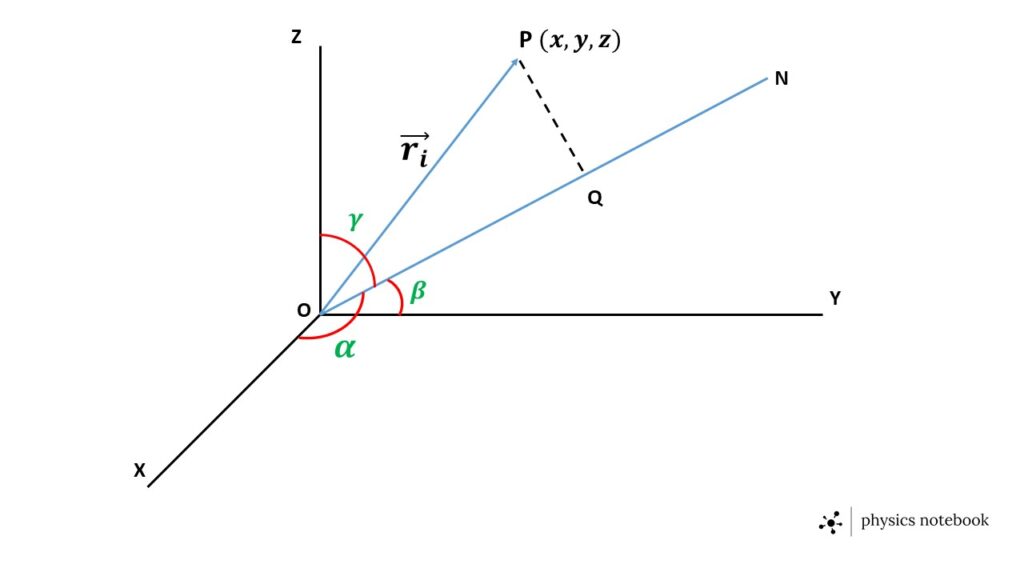
Now, given that, \( \cos\alpha \), \( \cos\beta \) and \( \cos\gamma \) are the direction cosine of the ON and PQ is drawn perpendicular to ON. So, \( \cos^2\alpha+\cos^2\beta+\cos^2\gamma=1 \)

Now the moment of inertia of the body about the axis ON is,

\( I=\sum{m_i}PQ^2=\sum{m_i}(OP^2-OQ^2) \)

Here, \( OP^2=r_i^2=(x_i^2+ y_i^2+ z_i^2) \)

The projection of OP on ON = OQ= \( (\cos\alpha)\ x_i+ (\cos\beta)\ y_i + (\cos\gamma)\ z_i \)= \( l\ x_i+m\ y_i+n\ z_i \)

Where, \( \cos\alpha=l \), \( \cos\beta=m \) and \( \cos\gamma=n \)

Therefore,

\( I=\sum{m_i}[(x_i^2+ y_i^2+ z_i^2)-(l\ x_i+m\ y_i+n\ z_i)^2 ] \) \( =\sum{m_i}[x_i^2+ y_i^2+ z_i^2- l^2\ x_i^2-m^2\ y_i^2-n^2\ z_i^2-2lmx_iy_i-2mny_iz_i-2nlz_ix_i] \) \( =\sum{m_i}[(1-l^2)x_i+(1-m^2)y_i+(1-n^2)z_i-2lmx_iy_i-2mny_iz_i-2nlz_ix_i] \) \( =\sum{m_i}[(m^2+n^2)x_i+(n^2+l^2)y_i+(l^2+m^2)z_i-2lmx_iy_i-2mny_iz_i-2nlz_ix_i] \) \( =\sum{m_i}[l^2(y_i^2+z_i^2)+m^2(z_i^2+x_i^2)+n^2(x_i^2+y_i^2) -2lmx_iy_i-2mny_iz_i-2nlz_ix_i] \) \( = l^2\sum{m_i} (y_i^2+z_i^2)+m^2\sum{m_i} (z_i^2+x_i^2)+n^2\sum{m_i} (x_i^2+y_i^2)\\+2lm(-\sum{m_i}x_iy_i)+2mn(-\sum{m_i}y_iz_i)+2nl(-\sum{m_i}z_ix_i) \)

\( or,\ I=l^2I_{xx}+m^2I_{yy}+n^2I_{zz}+2lmI_{xy}+2mnI_{yz}+2nlI_{zx} \)

\( Or,\ I=I_{xx}\ \cos^2\alpha+I_{yy}\ \cos^2\beta+I_{zz}\ \cos^2\gamma\\+2I_{xy}\cos\alpha\ \cos\beta+2I_{yz}\cos\beta\ \cos\gamma+2I_{zx}\cos\gamma\ \cos\alpha \)

If the original axes are the principal axes, then we can write,

\( I_{xy}=I_{yz}=I_{zx}=0 \)

Now the moment of inertia of the body is,

\( I=I_{xx}\ \cos^2\alpha+I_{yy}\ \cos^2\beta+I_{zz}\ \cos^2\gamma \)