Kinetic energy of rotating body:
Let us consider a rigid body of mass M is rotating about a fixed axis \( O_1O_2 \) with an uniform angular velocity \( \omega \).
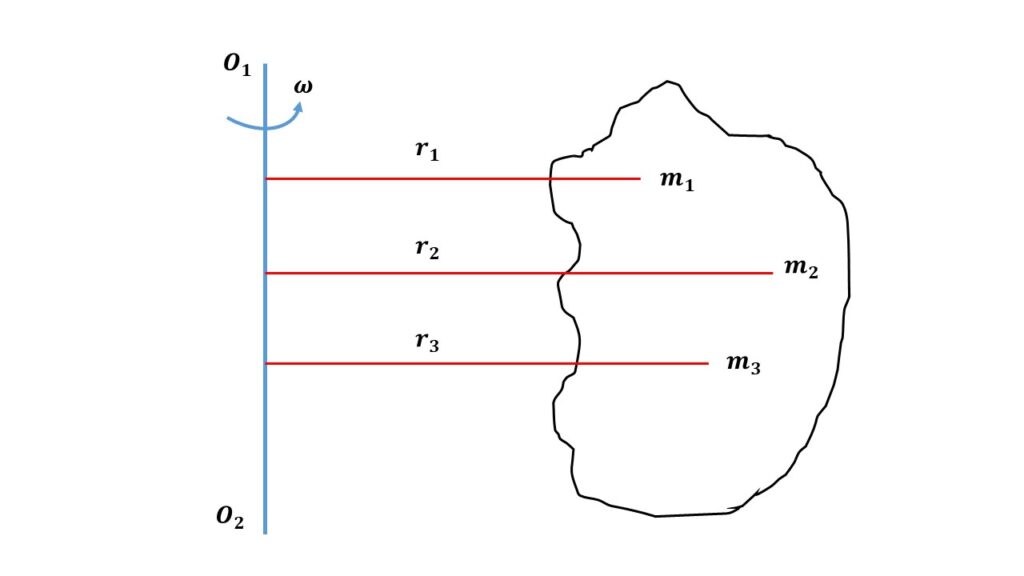
Let us consider, the rigid body consists of a large number of particles of masses \( m_1 \), \( m_2 \), \( m_3 \) etc, situated at distances \( r_1 \), \( r_2 \), \( r_3 \) etc, respectively from the axis of rotation, as shown in the figure. Since the rigid body moves with an angular velocity \( \omega \), so all the particles moves with the same angular velocity \( \omega \). But the linear velocities of the particles are different, because the distances of the particles are not same. So the respective linear velocities of the particles are \( v_1=r_1\omega \), \( v_2=r_2\omega \), \( v_3=r_3\omega \) etc.
Now the total kinetic energy of the whole body is given by,
\( E=\frac{1}{2}m_1{v_1}^2+\frac{1}{2}m_2{v_2}^2+\frac{1}{2}m_3{v_3}^2+\cdots \\=\frac{1}{2}m_1{r_1}^2{\omega}^2+\frac{1}{2}m_2{r_2}^2{\omega}^2+\frac{1}{2}m_3{r_3}^2{\omega}^2+\cdots\\=\frac{1}{2}{\omega}^2(m_1{r_1}^2+m_2{r_2}^2+m_3{r_3}^2+\cdots)\\=\frac{1}{2}{\omega}^2\sum(mr^2)\\=\frac{1}{2}I{\omega}^2\)Where, \( I=\sum{mr^2} \) is the moment of inertia of the body about the axis of rotation.