(i) Moment of inertia of a uniform solid sphere about one of its diameter:

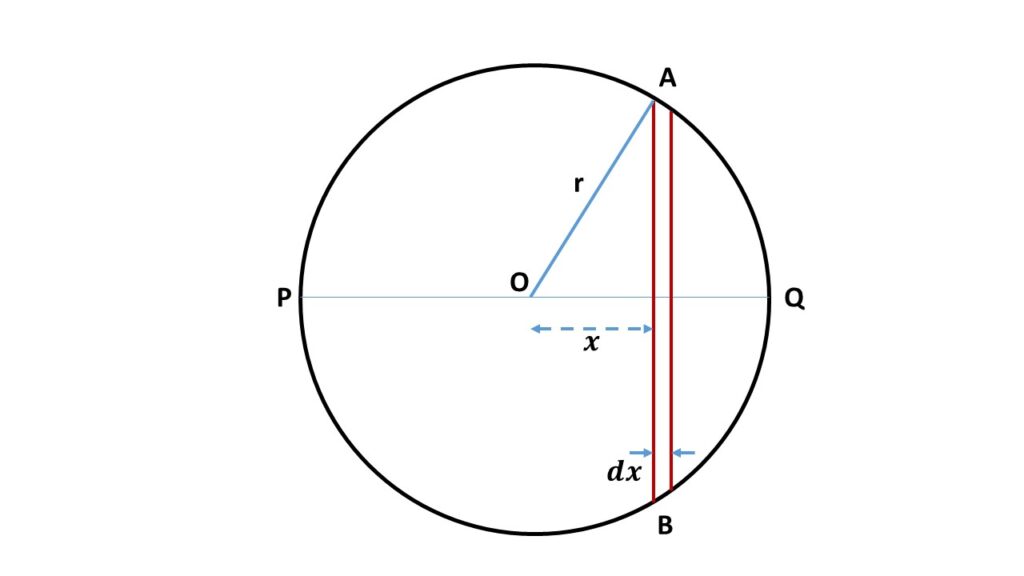
Let us consider a uniform solid sphere of radius r and mass M, rotating about one of its own diameter PQ. So the volume of this solid sphere is \( \frac{4}{3}\pi{r}^2 \) and the mass density i.e., mass per unit volume is \( \frac{M}{\frac{4}{3}\pi{r}^3} \).

To calculate the moment of inertia of this solid uniform sphere about the diameter PQ, let us consider an elementary circular disc AB at a distance \( x \) from the centre O of the sphere, and of thickness \( dx \). Radius of this elementary disc is \( \sqrt{r^2-x^2} \) and the volume is \( \pi(r^2-x^2)dx \). So the mass of this elementary disc is \( \frac{M}{\frac{4}{3}\pi{r}^3}\times\pi(r^2-x^2)dx \) = \( \frac{3M}{4r^3}(r^2-x^2)dx \).
The moment of inertia of this circular elementary disc about the diameter PQ is
\( \frac{1}{2}\left(\frac{3M}{4r^3}(r^2-x^2)dx\right){(\sqrt{r^2-x^2})}^2 \)
= \( \frac{3M}{8r^3}{(r^2-x^2)}^2dx \)

So the moment of inertia of this whole solid uniform sphere about the diameter PQ is given by,

\( I=\displaystyle{\int_{-r}^{r}}\frac{3M}{8r^3}{(r^2-x^2)}^2dx \)

or, \( I=2\frac{3M}{8r^3}\displaystyle{\int_0^r}{(r^2-x^2)}^2dx \)

or, \( I=\frac{3M}{4r^3}\displaystyle{\int_0^r}\left(r^4-2r^2x^2+x^4\right)dx \)

or, \( I=\frac{3M}{4r^3}{\left(r^4x-\frac{2}{3}r^2x^3+\frac{x^5}{5}\right)}_0^4 \)

or, \( I=\frac{3M}{4r^3}\left(r^5-\frac{2r^5}{3}+\frac{r^5}{5}\right) \)

or, \( I=\frac{3M}{4r^3}\frac{8}{15}r^5 \)

or, \( I=\frac{2}{5}Mr^2 \)

(ii) Moment of inertia of the uniform solid sphere about a tangent:

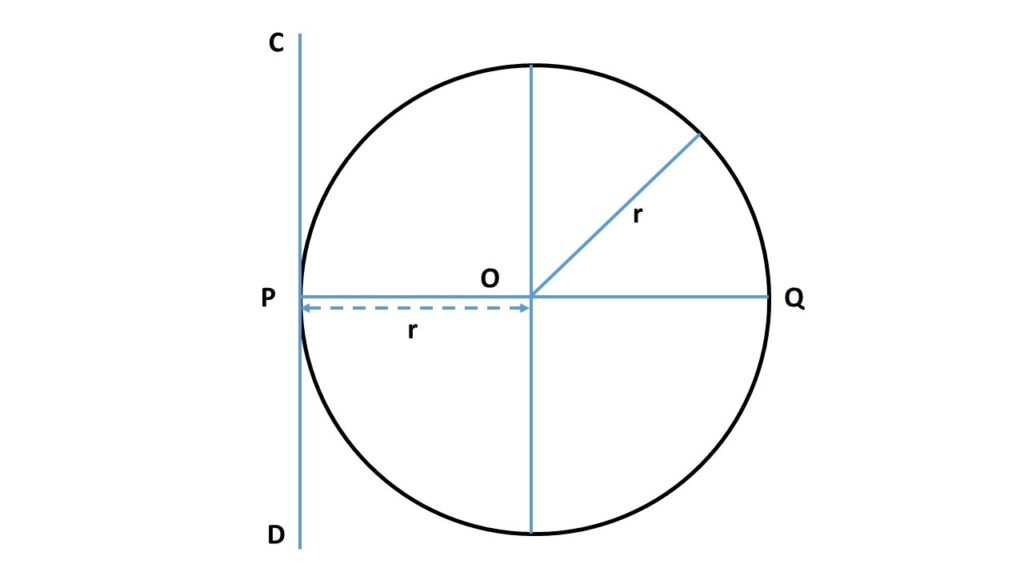
Let us consider the solid uniform sphere is rotating about an axis CD which is a tangent of the sphere and parallel to the diameter of the sphere. So by applying the theorem of parallel axis we can write that the moment of inertia of this solid sphere about the tangent CD is

\( I_{CD}=\frac{2}{5}Mr^2+Mr^2 \)

or, \( I_{CD}=\frac{7}{5}Mr^2 \)

(iii) Moment of inertia of a solid uniform sphere about its centre:

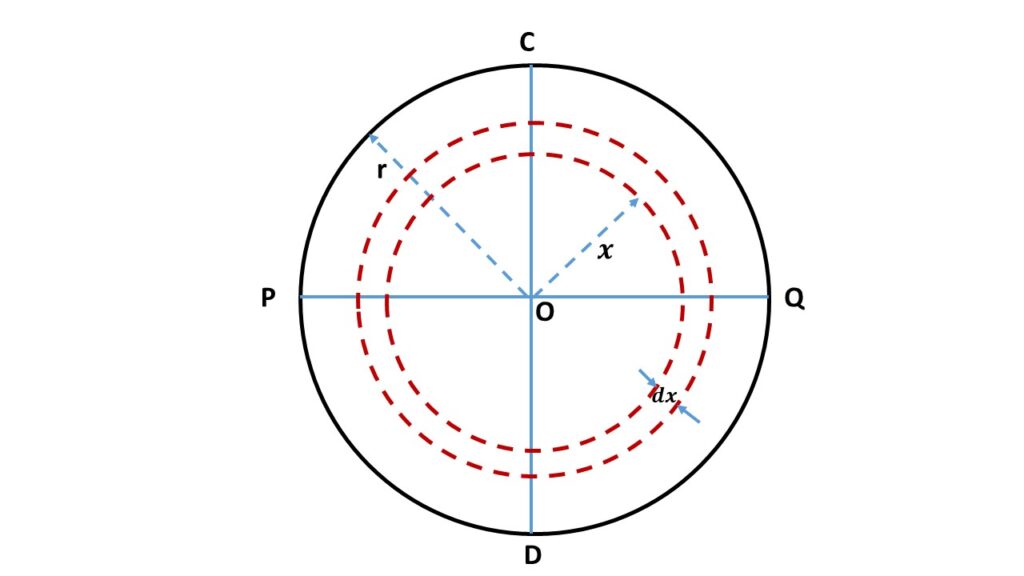
Let us consider a solid sphere of radius r and mass M. So the volume of this sphere is \( \frac{4}{3}\pi{r^3} \) and the mass density i.e., the mass per unit volume of this sphere is \( \frac{M}{\frac{4}{3}\pi{r^3}} \). In order to calculate the moment of inertia of this sphere about its centre O, let us consider a concentric spherical shell of radius \( x \) and thickness \( dx \). So the volume of this concentric spherical shell is \( 4\pi{x^2}dx \) and the mass is \( \frac{M}{\frac{4}{3}\pi{r^3}}\times{4\pi{x^2}dx} \) = \( \frac{3M}{r^3}x^2{dx} \). Therefore the moment of inertia aof this spherical shell about the centre O is \( \frac{3M}{r^3}x^2{dx}\times{x^2} \) = \( \frac{3M}{r^3}x^4{dx} \).

Now the moment of inertia of this whole uniform solid sphere about the centre O is given by,

\( I_0=\displaystyle{\int_0^r}\frac{3M}{r^3}x^4{dx} \)

or, \( I_0=\frac{3M}{r^3}\left(\frac{x^5}{5}\right)_0^r \)

or, \( \displaystyle{I_0= \frac{3}{5}Mr^2} \)