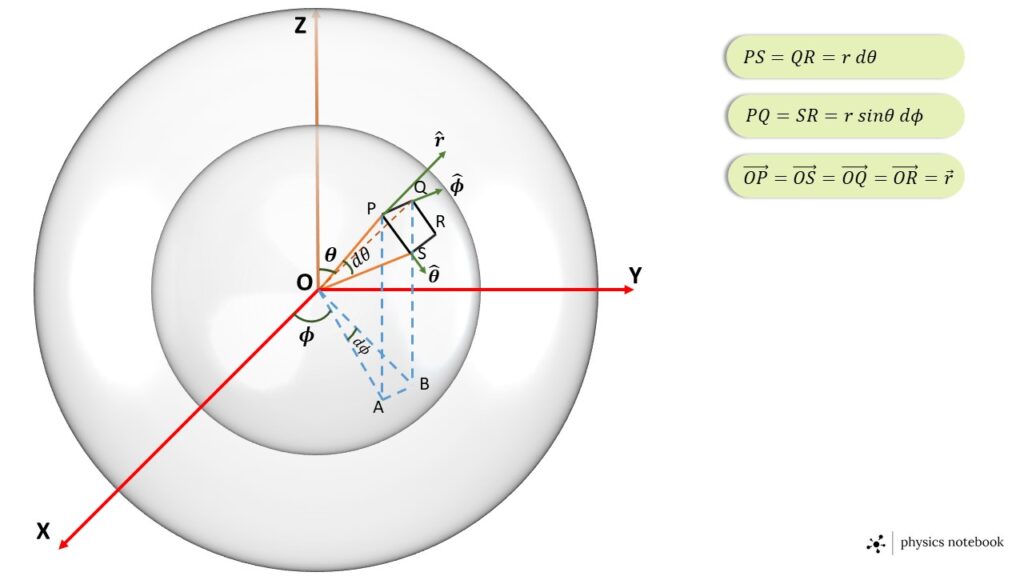
Let us consider a very small volume element PQRSS’P’Q’R as shown in Fig.1. The lower surface PQRS of this volume element lies on the surface of the sphere of radius \( r \) and the parallel surface P’Q’R’S’ lies on the surface of the sphere of radius \( (r+dr) \). Since the angles \( d\theta \) and \( d\phi \) and radial extension \( dr \) are very small, so the volume element can be assumed as rectangular volume element.

Area element in the spherical polar co-ordinate system:

The radial co-ordinate of each point on the area element PQRS is \( r \).

The co-ordinates of the point P with respect to the origin O are \( r,\ \theta,\ \phi \)

The co-ordinates of the point S with respect to the origin O are \( r,\ \theta+d\theta,\ \phi \)

The co-ordinates of the point Q with respect to the origin O are \( r,\ \theta,\ \phi+d\phi \)

Now from Fig.1, we can write,

\( PS=QR=r\ d\theta \) and \( PQ=SR=r\ \sin\theta\ d\phi \)

Again the radial co-ordinate of each point on the parallel area element P’Q’R’S’ is \( (r+dr) \)

The co-ordinates of the point P’ with respect to the origin O are \( r+dr,\ \theta,\ \phi \)

The co-ordinates of the point S’ with respect to the origin O are \( r+dr,\ \theta+d\theta,\ \phi \)

The co-ordinates of the point Q’ with respect to the origin O are \( r+dr,\ \theta,\ \phi+d\phi \)

The rectangular parallelopiped PQRSS’P’Q’R’ has three pairs of area elements, which are given bellow:

• Area PQRS = area P’Q’R’S’
• Area PP’Q’Q = area SS’R’R
• Area PP’S’S = area QQ’R’R

Area PQRS:

Since the radial distance of each point of area PQRS is the same, so \( r \) is constant but \( \theta \) and \( \phi \) are variable. The two vectors \( \vec{PQ} \) and \( \vec{PS} \) represent the two side of the area PQRS, as shown in the Fig. 2.

From Fig. 2 the vector \( \vec{PQ} \) can be writte as, \( \vec{PQ}=r\ \sin\theta\ d\phi\ \hat{\phi} \),

where, the magnitude of the vector \( \vec{PQ} \) is, \( |\vec{PQ}|=r\ \sin\theta\ d\phi \)

and the the direction is along the unit vector \( \hat{\phi} \).

Again the vector \( \vec{PS} \) can be witten as, \( \vec{PS}=r\ d\theta\ \hat{\theta} \),

where, the magnitude of the vector \( \vec{PS} \) is \( |\vec{PS}|=r\ d\theta \)

and the direction is along the unit vector \( \hat{\theta} \).

Therefore the area of PQRS is

\( {d\vec{A}}_r=\vec{PS}\times\vec{PQ}=(r\ d\theta\ \hat{\theta})\times(r\ \sin\theta\ d\phi\ \hat{\phi}) \)

\( or,\ {d\vec{A}}_r=r^2\ \sin\theta\ d\theta\ d\phi\ (\hat{\theta}\times\hat{\phi}) \)

\( or,\ {d\vec{A}}_r=r^2\ \sin\theta\ d\theta\ d\phi\ \hat{r} \)

where, unit vectors \( \hat{r} \), \( \hat{\theta} \) and \( \hat{\phi} \) are constituted in a right handed orthogonal co-ordinate system, as a result, \( \hat{\theta}\times\hat{\phi}=\hat{r} \).

Here the area PQRS has a magnitude \( r^2\ \sin\theta\ d\theta\ d\phi \) and the direction of that area is along the unit vector \( \hat{r} \). This means that the surface PQRS is in the plane containing the unit vectors \( \hat{\theta} \) and \( \hat{\phi} \) and perpendicular to the unit vector \( \hat{r} \).

Area PP’Q’Q:

Here \( \theta \) is constant for each point on the area PP’Q’Q but \( r \) and \( \phi \) are variable. The two vectors \( \vec{PQ} \) and \( \vec{PP'} \) represent the two side of the area PP’Q’Q, as shown in the Fig. 3.

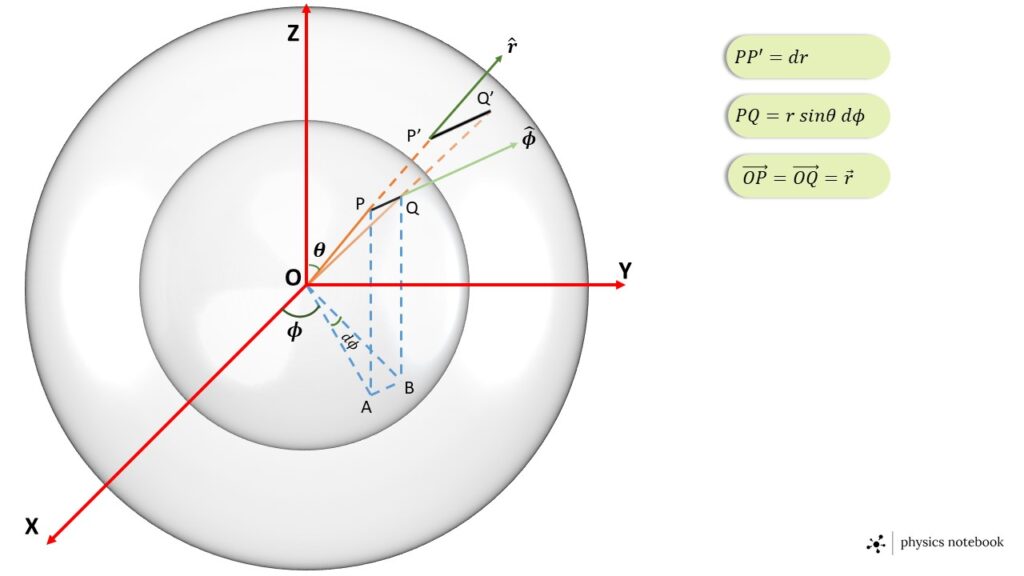
From Fig. 3 the vector \( \vec{PQ} \) can be writte as, \( \vec{PQ}=r\ \sin\theta\ d\phi\ \hat{\phi} \),

where, the magnitude of the vector \( \vec{PQ} \) is, \( |\vec{PQ}|=r\ \sin\theta\ d\phi \)

and the the direction is along the unit vector \( \hat{\phi} \).

Again the vector \( \vec{PP'} \) can be witten as, \( \vec{PP'}=dr\ \hat{r} \),

where, the magnitude of the vector \( \vec{PP'} \) is \( |\vec{PP'}|=dr \)

and the direction is along the unit vector \( \hat{r} \).

So the area of PP’Q’Q is given by,

\( {d\vec{A}}_{\theta}=\vec{PQ}\times\vec{PP'}=(r\ \sin\theta\ d\phi\ \hat{\phi})\times(dr\ \hat{r}) \)

or, \( {d\vec{A}}_{\theta}=r\ \sin\theta\ d\phi\ dr\ (\hat{\phi}\times\hat{r}) \)

or, \( {d\vec{A}}_{\theta}=r\ \sin\theta\ d\phi\ dr\ \hat{\theta} \)

where, unit vectors \( \hat{r} \), \( \hat{\theta} \) and \( \hat{\phi} \) are constituted in a right handed orthogonal co-ordinate system, as a result, \( (\hat{\phi}\times\hat{r})=\hat{\theta} \).

Here the area PP’Q’Q has a magnitude \( r\ \sin\theta\ d\phi\ dr \) and the direction of that area is along the unit vector \( \hat{\theta} \). This means that the surface PP’Q’Q is in the plane containing the unit vectors \( \hat{r} \) and \( \hat{\phi} \) and perpendicular to the unit vector \( \hat{\theta} \).

Area PP’S’S:

Here \( \phi \) is constant for each point on the area PP’S’S but \( r \) and \( \theta \) are variable. The two vectors \( \vec{PS} \) and \( \vec{PP'} \) represent the two side of the area PP’S’S, as shown in the Fig. 4.

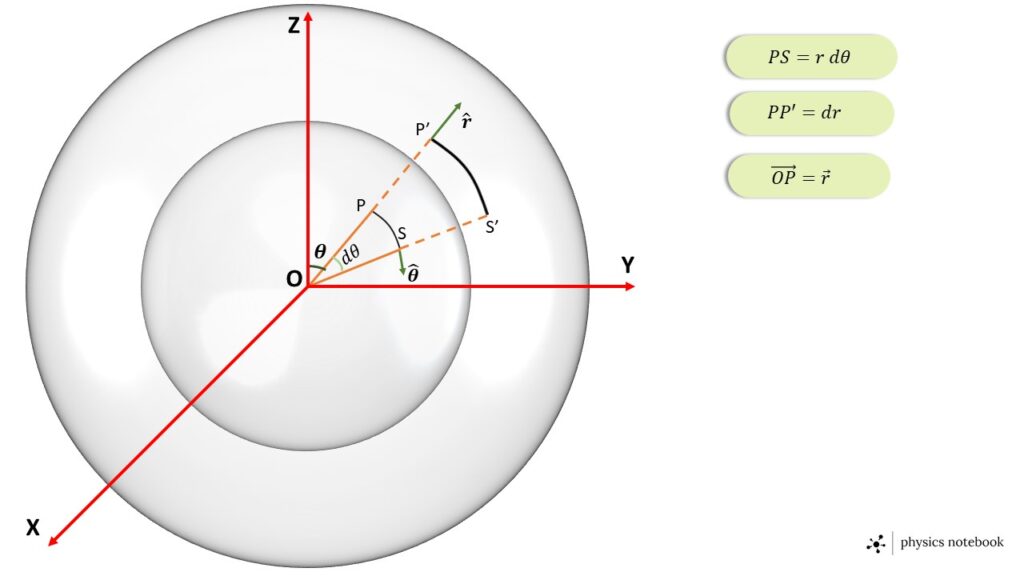
From Fig. 3 the vector \( \vec{PS} \) can be writte as, \( \vec{PS}=r\ d\theta\ \hat{\theta} \),

where, the magnitude of the vector \( \vec{PS} \) is, \( |\vec{PS}|=r\ d\theta \)

and the the direction is along the unit vector \( \hat{\theta} \).

Again the vector \( \vec{PP'} \) can be witten as, \( \vec{PP'}=dr\ \hat{r} \),

where, the magnitude of the vector \( \vec{PP'} \) is \( |\vec{PP'}|=dr \)

and the direction is along the unit vector \( \hat{r} \).

So the area of PP’S’S is given by,

\( {d\vec{A}}_{\phi}=\vec{PP'}\times\vec{PS}=(dr\ \hat{r})\times(r\ d\theta\ \hat{\theta}) \)

or, \( {d\vec{A}}_{\phi}=r\ dr\ d\theta(\hat{r}\times\hat{\theta}) \)

or, \( {d\vec{A}}_{\phi}=r\ dr\ d\theta\ \hat{\phi} \)

Here the area PP’S’S has a magnitude \( r\ dr\ d\theta \) and the direction of that area is along the unit vector \( \hat{\phi} \). This means that the surface PP’S’S is in the plane containing the unit vectors \( \hat{r} \) and \( \hat{\theta} \) and perpendicular to the unit vector \( \hat{\phi} \).