Relation between torque and moment of inertia:
Let us consider that a rigid body consists of a large number of particles of masses \( m_1 \), \( m_2 \), \( m_3 \), etc., rotating about a fixed axis \( O_1O_2 \) with a uniform angular acceleration \( \alpha =\frac{d\omega}{dt}\). Let \( r_1 \), \( r_2 \), \( r_3 \), etc. be the distances of the masses \( m_1 \), \( m_2 \), \( m_3 \), etc respectively from the axis of rotation
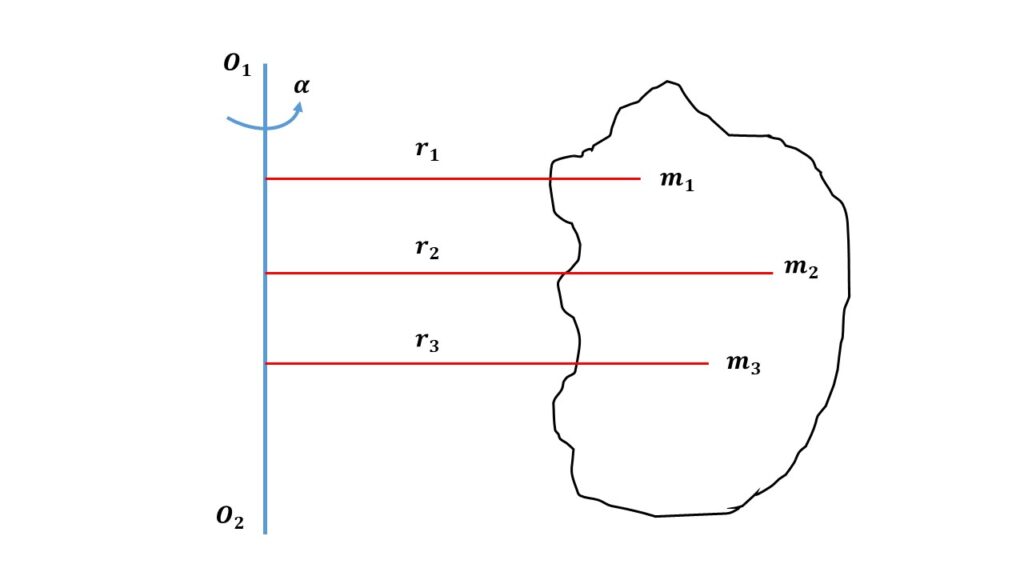
The linear acceleration of the particle of mass \( m_1 \) is \( r_1\alpha \), so the force acting on this particle is \( m_1r_1\alpha \). The moment of this force about the axis of rotation is \( m_1r_1\alpha\times{r_1}=m_1{r_1}^2\alpha \). This moment of force is also known as the torque.
Now, the torque acting on mass \( m_2 \) is \( m_2{r_2}^2\alpha \), the torque acting on the mass \( m_3 \) is \( m_3{r_3}^2\alpha \) and so on.
So the total torque acting on the entire rigid body is given by,
\( \tau=m_1{r_1}^2\alpha+m_2{r_2}^2\alpha+m_3{r_3}^2\alpha+m_{r_3}^2\alpha+\cdots\\=(m_1{r_1}^2+m_2{r_2}^2+m_3{r_3}^2+\cdots)\alpha\\=(\sum{mr^2})\alpha\\=I\alpha \)
where, \( I=\sum{mr^2} \) is the moment of inertia of he body about the axis of rotation.