In a two-dimensional plane polar co-ordinate system, there are two unit vectors$\cdots$

1. The radial unit vector  $\hat{r}$. The direction of this unit vector is along the radius vector  $\vec{r}$
2. The unit vector  $\hat{\theta}$ along the direction of increasing $\theta$.

Similarly, in case of planer motion in a two-dimensional Cartesian co-ordinate system, there are also two unit vectors,

1. The unit vector $\hat{i}$ along the direction of the X-axis.
2. The unit vector $\hat{j}$ along the direction of the Y-axis

Relations:

• The unit vector $\hat{r}$ in term of the unit vectors $\hat{i}$ and $\hat{j}$ :
  Let, In two dimensional cartesian co-ordinate system, $(x,y)$ be the position vector of the point $A$
  And, in plane polar co-ordinate system, ( $\hat{r}$, $\theta$ ) be the position vector of the same point $A$, as shown in the figure 1.1.
  Here, $\vec{OA}=\vec{r}$.
  So the unit vector $\hat{r}$ is along the direction of the vector $\vec{r}$, i.e., $\vec{OA}$. The unit vector $\hat{\theta}$ is perpendicular to the $vec{OA}$.
  The unit vector $\displaystyle{\hat{r}=\frac{\vec{r}}{|\vec{r}|}}$, where, $|\vec{r}|$ is the modulus of the vector $\vec{r}$.
  Now, $\vec{r}=x\hat{i}+y\hat{j}$
  Again, $x=r\cos\theta$ & $y=r\sin\theta$
  therefore, $\vec{r}=r\cos\theta\hat{i}+r\sin\theta\hat{j}$
  so the unit vector, $\displaystyle{\hat{r}=\frac{\vec{r}}{|\vec{r}|}=\frac{ r\cos\theta\hat{i}+r\sin\theta\hat{j}}{r}}$
  or, $\hat{r}=\cos\theta\hat{i}+\sin\theta\hat{j}$.

• The unit vector $\hat{\theta}$ in term of the unit vectors $\hat{i}$ and $\hat{j}$ :
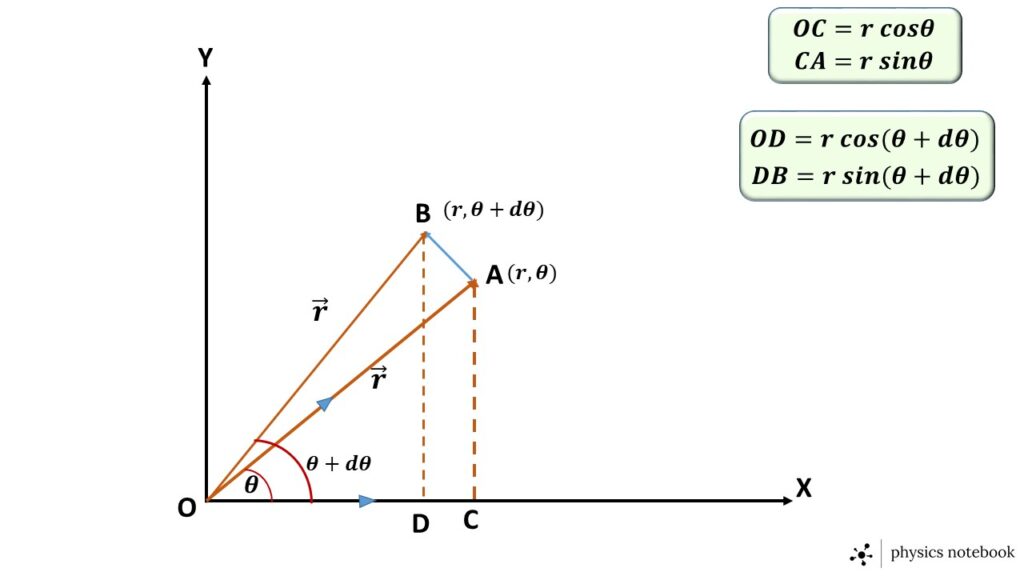
  Let us consider a point $A$ having polar co-ordinate $(r,\theta)$ & another point $B$ having polar co-ordinate $(r,\theta+d\theta)$, as shown in the adjoining figure 1.2.
  $\vec{OA}=r\cos\theta\hat{i}+r\sin\theta\hat{j}$
  and, $\vec{OB}=r\cos(\theta+d\theta)\hat{}+r\sin(\theta+d\theta)\hat{j}$
  Again, $\vec{AB}=\vec{OA}-\vec{OB}$.
  or, $\vec{AB}= r\cos\theta\hat{i}+r\sin\theta\hat{j}- r\cos(\theta+d\theta)\hat{}+r\sin(\theta+d\theta)\hat{j}$
  or, $\vec{AB}=r[\cos(\theta+d\theta)-\cos\theta]\hat{i}+r[\sin(\theta+d\theta)-\sin\theta]\hat{j}$
  or $\vec{AB}=-r\ \sin\theta\ d\theta\hat{i}+r\ \cos\theta\ d\theta\hat{j}$
  
  Where, $\cos(\theta+d\theta)-\cos\theta=\cos\theta\ \cos{d\theta}-\sin\theta\ \sin{d\theta}-\cos\theta$
  or, $\cos(\theta+d\theta)-\cos\theta=-\sin\theta\ d\theta$
  [ Since, $d\theta$ is very small. So $\cos{d\theta}=1$ and $\sin{d\theta}=d\theta$ ]
  Similarly, $\sin(\theta+d\theta)-\sin\theta=\sin\theta\ \cos{d\theta}-\cos\theta\ \sin{d\theta}-\sin\theta$
  or, $\sin(\theta+d\theta)-\sin\theta =\cos\theta\ d\theta$
  
  The direction of the vector $\vec{AB}$ is along the direction of the increasing $\theta$.
  The magnitude of the vector $\vec{AB}$ is,
  $|\vec{AB}|=r\ d\theta\sqrt{({\sin}^2\theta+{\cos}^2\theta)}=r\ d\theta$
  The unit vector
  $\displaystyle{\hat{\theta}=\frac{\vec{AB}}{|\vec{AB}|}}$
  or, $\displaystyle{\hat{\theta}=\frac{-r\ \sin\theta\ d\theta\hat{i}+r\ \cos\theta\ d\theta\hat{j}}{r\ d\theta}}$
  or, $\hat{\theta}=-\sin\theta\hat{i}+\cos\theta\hat{j}$

The polar unit vectors vary from point to point, they are not fixed like $\hat{i}$ and $\hat{j}$. When a point moves, the polar unit vectors become a function of time.