Coefficient of viscosity:
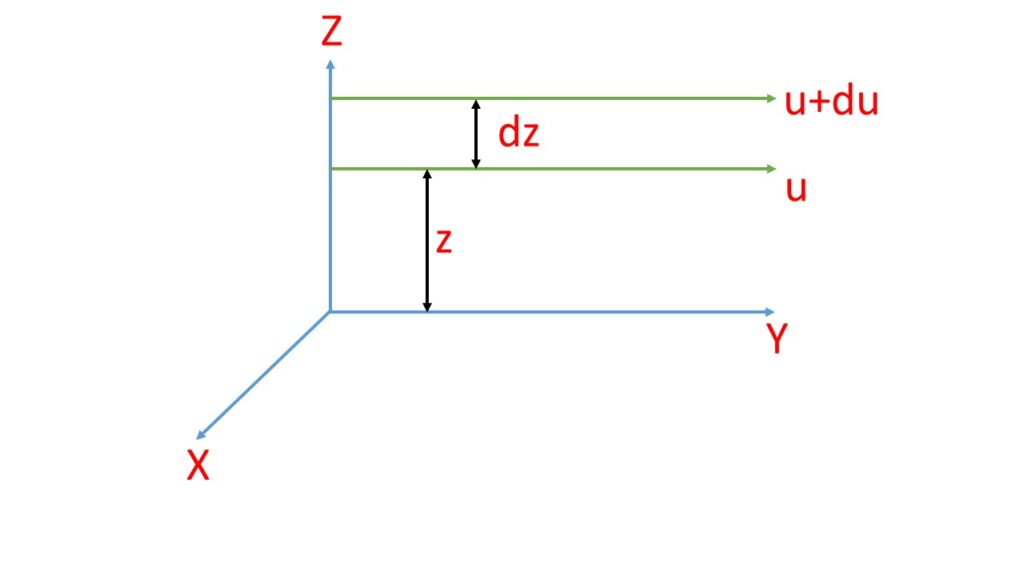
Let us consider a region of a liquid flowing in streamline motion parallel to the X-Y plane along the positive Y direction. Let us consider two adjacent layers at a distance z and z+dz from the fixed layer above the X-Y plane. The velocities of these two adjacent layers are u and u+du respectively, as shown in the adjoining Fig. 1. So the velocity gradient is \( \frac{du}{dz} \).
If \( F \) be the backward dragging force or viscous force acting tangentially between the two layers and if \( A \) be the area of contact over which it acts, then
where, \( \eta \) is the proportioality constant. It is called the coefficient of viscosity.
The negative sign indicates that the direction of force is opposite to that of the viscosity of the liquid.
We can write,
\( \displaystyle{\eta=-\frac{F}{A\cdot\frac{du}{dz}}} \)This is known as Newton’s law of viscous flow for the streamline motion.
If \( A=1 \) and \( \frac{du}{dz}=1 \), then \( \eta=F \)(numerically)
Therefore, the coefficient of viscosity of a liquid is defined as the tangential force per unit area required to maintain a unit velocity gradient.
Dimension:
The dimension of \( \eta \) is \( \displaystyle{\frac{MLT^{-2}}{L^2\frac{LT^{-1}}{L}} =ML^{-1}T^{-1}} \)
Units of \( \eta \):
The unit of \( \eta \) are poise or \( dyne-s-cm^{-2} \) in c.g.s. unit,
and decapoise or \( N-S-m^{-2} \) in S.I. unit.