Solid Angle:

The solid angle subtended by a surface at a point is measured by the ratio of the normal component of the area of the surface to the square of the distance of the surface from the point.

Let us consider \( d\omega \) be the solid angle at a point O, subtended by the area \( d\vec{A} \). The area \( d\vec{A} \) is at a distance r from the point O, then we can write

\( \displaystyle{d\omega=\frac{d\vec{A}\cdot\hat{r}}{r^2}=\frac{|d\vec{A}|\ \cos\alpha}{r^2}} \)

where \( \hat{r} \) is the unit vector along the direction of \( \vec{r} \), \( {\alpha} \) is the angle between the radial vector \( \vec{r} \) and the area vector \( d\vec{A} \).

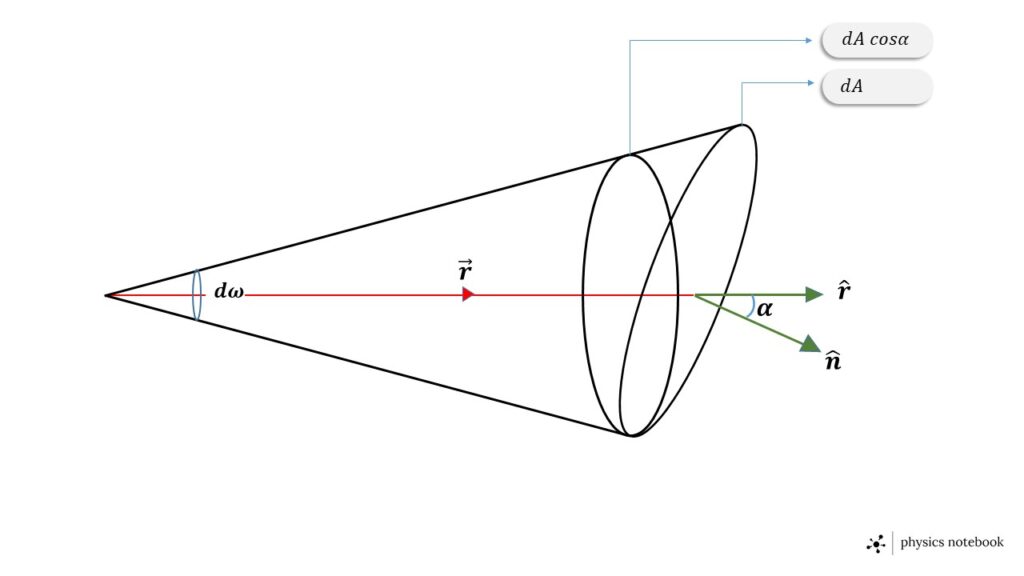
When the angle \( \alpha \) between \( d\vec{A} \) and \( \vec{r} \) is \( 0^{\circ} \), i.e., the surface area \( d\vec{A} \) is normal to the line joining any point on the boundary on the surface area to the point O, then the solid angle will be,

\( \displaystyle{d\omega=\frac{dA}{r^2}} \)

Dimension of solid angle:

Since the solid angle is the ratio of two same dimensions, so the solid angle has no dimensions.

Unit of solid angle:

The unit of the solid angle is the steradian.

we know if \( \alpha=0^{\circ} \) then solid angle \( \displaystyle{d\omega=\frac{dA}{r^2}} \), again when \( dA=r^2 \) then, \( d\omega=1\ steradian \).

Steradian is defined as the solid angle at the centra of a sphere subtended by the surface area of that sphere, when the surface area of the sphere is equal to the square of the radius of the sphere.