Strain Energy:
When a body is strained, internal forces due to the elastic property of the body are set up and hence work must be done by the applied force against the internal forces. The work is stored up within the body as potential energy which is known as the energy of strain or strain energy.
Let us consider the work done during the three cases of strain:
(i) Tensile or longitudinal strain ( stretching of a wire ):
Let us consider a wire of length \( L \) and cross sectional area \( A \) fixed at the upper end. Let the wire is stretched by an amount \( l \) by a stretching force \( F \).
For a small increase in length \( dl \) of the wire the work done is \( dw=F\cdot{dl} \).
So the total work done for stretching the wire from 0 to \( l \) is
\( W=\displaystyle\int_0^l{F\cdot{dl}} \)Now Young’s Modulus of the material of the wire is
\( Y=\frac{F/A}{l/L}=\frac{FL}{Al} \)or, \( \displaystyle{F=\frac{YAl}{L}} \)
\( W=\displaystyle\int_0^l{ \frac{YAl}{L} }dl \\=\frac{YA}{L}\displaystyle\int_0^l{l}dl \\=\frac{YA}{L}\frac{l^2}{2} \)or, \( W=\frac{1}{2}\frac{YAl}{L}l\\=\frac{1}{2}Fl \)
or, \( W=\frac{1}{2} \) \( \times \)stretching force \( \times \) stretch
(ii) Volume Strain:
If the volume \( V \) of a substance be subjected to an external pressure \( p \) and the corresponding volume change be \( v \) then the bulk modulus (\( K \)) is given by,
\( K=\frac{p}{v/V}=\frac{pV}{v} \),
or, \( p=\frac{Kv}{V} \)
Due to the application of this pressure the volume change \( v \) takes place by steps of \( dv \).
The work done in each step is given by \( dw=p\cdot{dv} \).
The total work done for the change in volume \( v \) is,
\( W=\displaystyle\int_0^v{p}\cdot{dv} \)or, \( W=\displaystyle\int_0^v\frac{Kv}{V}dv \\=\frac{K}{V}\frac{v^2}{2}\\=\frac{1}{2}\frac{Kv}{V}v\\=\frac{1}{2}pv \)
or, \( W=\frac{1}{2} \) \( \times \)stress\( \times \)change in volume
Therefore workdone per unit volume is
\( \frac{1}{2}\frac{pv}{V}=\frac{1}{2}\times{p}\times\frac{v}{V}\\=\frac{1}{2}\times{stress}\times{strain} \)(iii) Shearing Strain:
Let us consider a cube of edge \( L \) with its lower face \( DC \) is fixed and let \( F \) be the tangential force applied to the upper face \( AB \) so that the face \( ABCD \) is displaced into the position \( A’B’CD \) and produce a shearing angle \( \theta \).
The rigidity modulus \( \eta=\frac{F/\alpha}{\theta}=\frac{F}{\alpha\theta} \)
where \( \alpha \) is the cross sectional area = \( L^2 \)
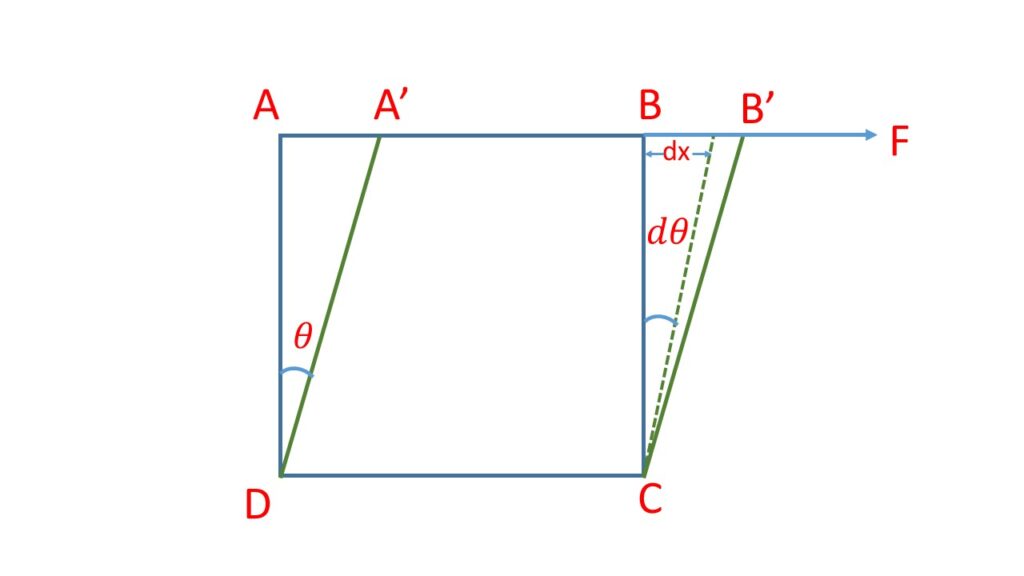
therefore, \( F=\eta\alpha\theta \).
The work done during a small shear \( d\theta \) and so for the small displacement \( dx \) is
\( dw=F\cdot{dx}=F\cdot{L}{d\theta} \)Therefore the total work done during the shear \( \theta \) is,
\( W=\displaystyle\int_0^{\theta}Fl\ d\theta\\=\displaystyle\int_0^{\theta}\alpha\eta{L}\theta\ d\theta\\=\alpha\eta{L}\frac{{\theta}^2}{2}\\=\frac{1}{2}\eta\alpha\theta\cdot{L}\theta\\=\frac{1}{2}FL\theta\\=\frac{1}{2}\times{tangential\ force}\times{displacement} \)Therefore the work done per unit volume is,
\( \frac{1}{2}\frac{FL\theta}{L^3}\\=\frac{1}{2}\frac{F}{L^2}\theta\\=\frac{1}{2}\frac{F}{\alpha}\theta\\=\frac{1}{2}\times{stress}\times{stress} \)