Calculate The Moment Of Inertia Of A Thin Uniform Rod (i) About An Axis Passing Through Its Centre And Perpendicular To Its Length, (ii) About An Axis Passing Through One Of Its End And Perpendicular To Its Length.

Share:

(i) Moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length:

Fig. 1

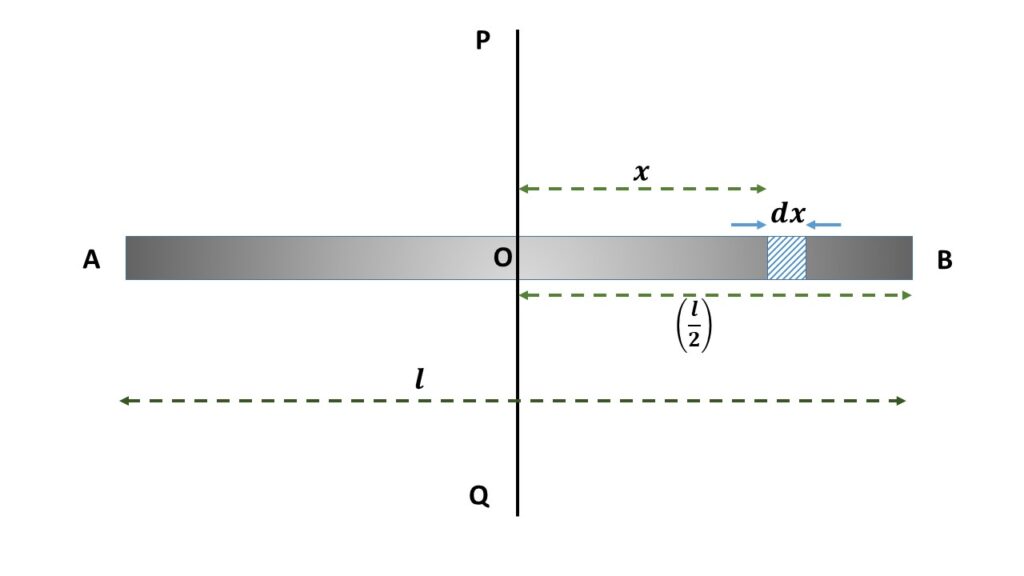
Let us consider a thin uniform rod AB of mass M and length \( l \). So the mass density i.e., mass per unit length of this rod is \( \left(\frac{M}{l}\right) \). In order to calculate the moment of inertia of the rod about an axis passing through its centre O and perpendicular to its length, let us consider an element of length \( dx \) at a distance \( x \) from the centre O. The mass of this element is \( \left(\frac{M}{l}dx\right) \) and the moment of inertia of this element about the axis PQ is \( \left(\frac{M}{l}dx\times{x^2}\right) \).

So the moment of inertia of the whole rod AB about the axis PQ is given by,

\( I=\displaystyle{\int_{-\frac{l}{2}}^{\frac{l}{2}}} \frac{M}{l}x^2\ dx \)

\( or,\ I=\frac{M}{3l}{(x^3)}_{-\frac{l}{2}}^{\frac{l}{2}} \)

\( or,\ I=\frac{M}{3l}\left[\frac{l^3}{8}+\frac{l^3}{8} \right] \)

\( or,\ \displaystyle{I=\frac{1}{12}Ml^2} \)

(ii) Moment of inertia of the thin rod about an axis passing through one of its ends and perpendicular to its length:

Method-I :

Fig. 2

Since the axis CD is parallel to the axis PQ at a perpendicular distance \( \left(\frac{l}{2}\right) \) from the axis PQ, so by applying the theorem of parallel axes, we can write that the moment of inertia of the rod about the axis CD passing through one ends of the rod and perpendicular to its length is given by,

\( I_{CD}= I+M{\left(\frac{l}{2}\right)}^2 \)
\( or,\ I_{CD}=\frac{1}{12}Ml^2+\frac{Ml^2}{4} \)
\( or,\ \displaystyle{I_{CD}=\frac{1}{3}Ml^2} \)

Method-II :

Fig. 3

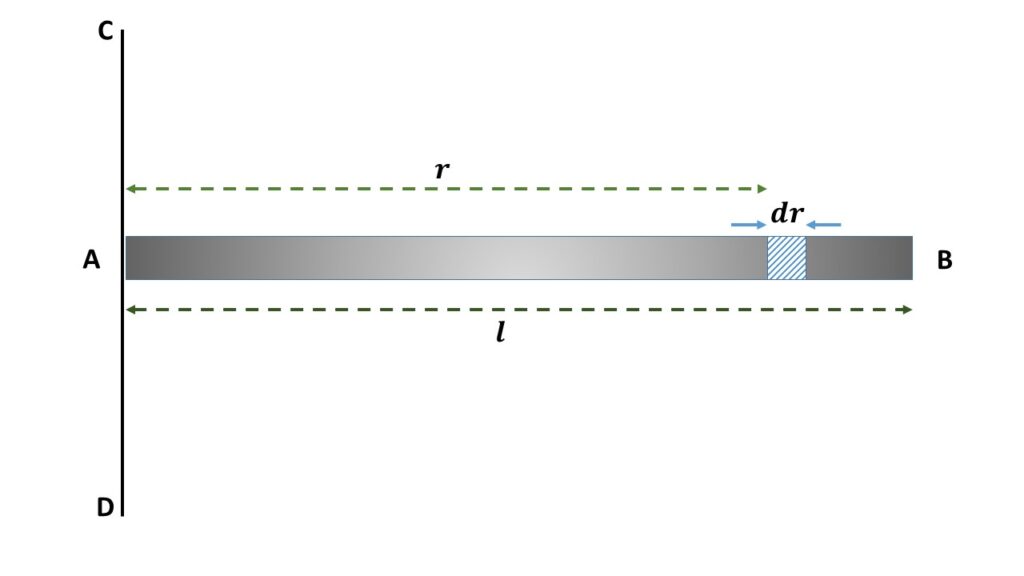
Let us consider a thin uniform rod AB of length \( l \) and mass M. So the mass density i.e., mass per unit length of this rod is \( \left(\frac{M}{l}\right) \). In order to calculate the moment of inertia of this rod about an axis CD passing through the end A and perpendicular to the length of this rod, let us consider an elementary length \( dr \) at a distance \( r \) from the end A. So the mass of this elementary length is \( \left(\frac{M}{l}\right)dr \) and the moment of inertia of this elementary length about the axis CD is \( \left(\frac{M}{l}\right){r^2}dr \).

So the moment of inerlia of this whole rod about the axis CD is given by,

\( I_{CD}=\displaystyle{\int_0^l}\left(\frac{M}{l}\right){r^2}dr \)

\( or,\ I_{CD}=\frac{M}{l}\displaystyle{\int_0^l}r^2{dr} \)

\( or,\ I_{CD}=\frac{M}{l}\frac{1}{3}{\left[r^3\right]}_0^l \)

\( or,\ \displaystyle{I_{CD}=\frac{1}{3}Ml^2} \)

Share:
Tags: ,