Moment of inertia of a thin spherical shell about a diameter:

Let us consider, a spherical shell of radius r and mass M. The surface area of this spherical shell is \( 4\pi{r^2} \). So the mass density i.e., mass per unit area of this spherical shell is \( \frac{M}{4\pi{r^2}} \).

In order to calculate the moment of inertia of this spherical shell about one of its diameter EF, let us consider a thin circular element ABDC of thickness \( r\cdot{d\phi} \) at a distance \( x \) from the centre \( O \) of the spherical shell, as shown in Fig. 1. The radius of this thin circular element is \( r_1=r\cos\phi \). So the surface area of this element is

\( 2\pi{r_1}\cdot{r\ {d\phi}}\\=2\pi(r\cos\phi)r\ {d\phi}\\=2\pi{r^2}\cos\phi\ {d\phi}\\=2\pi{r}\cdot{dx} \)

The mass of this element is \( \frac{M}{4\pi{r^2}}2\pi{r}\cdot{dx} \) = \( \frac{M}{2r}dx \)

The moment of inertia of this element about the axis EF is \( \frac{M}{2r}dx\cdot{r_1}^2 \) = \( \frac{M}{2r}\cdot{\left(\sqrt{{OA}^2-x^2}\right)}^2 \) = \( \frac{M}{2r}dx\left(r^2-x^2\right) \)

The moment of inertia of the whole shell about the diameter \( EF \) is

\( I=\displaystyle{\int_{-r}^{r}}\frac{M}{2r}\left(r^2-x^2\right)dx \)

\( =\frac{M}{2r}\left[\displaystyle{\int_{-r}^{r}}r^2{dx}-\displaystyle{\int_{-r}^{r}}x^2dx\right] \)

\( =\frac{M}{2r}\left[{(r^2x)}_{-r}^{r}-\frac{1}{3}{(x^3)}_{-r}^{r} \right] \)

\( =\frac{M}{2r}\left[r^2(r+r)-\frac{1}{3}(r^3+r^3)\right] \)

\( =\frac{M}{2r}\left(2r^3-\frac{2}{3}r^3\right) \)

\( or,\ I=\frac{2}{3}Mr^2 \tag{1}\)

(ii) Moment of inertia of a spherical shell about a tangent:

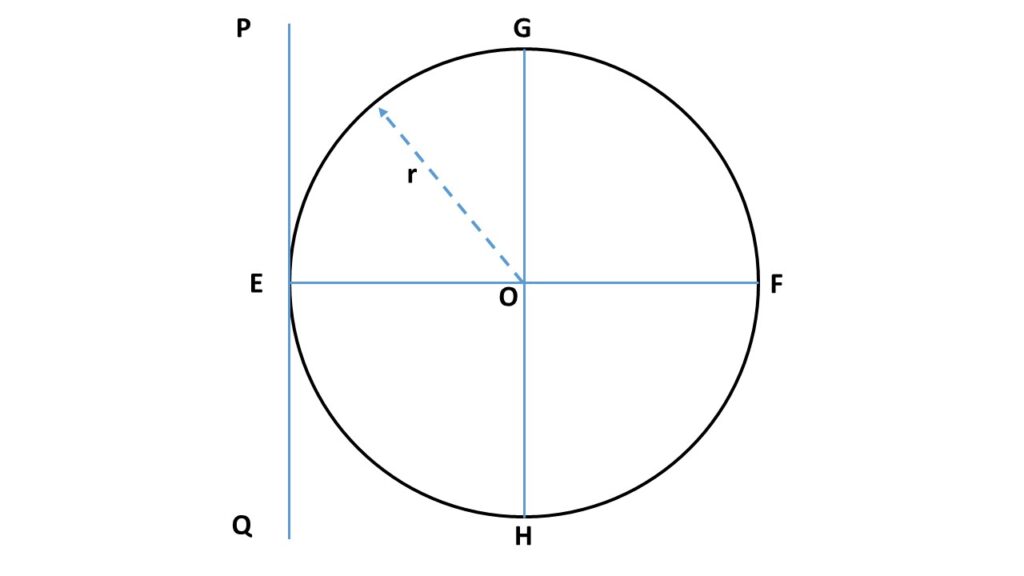
From the previous equation (1), we can write that the moment of inertia about the diameter GH is \( I=\frac{2}{3}Mr^2 \). By applying the theorem of parallel axes, the moment of inertia of the spherical shell about the tangent PQ, which is parallel to the diameter GH at a perpendicular distance \( r \) from the diameter GH, is given by

\( I_{PQ}=I+Mr^2\\or,\ I_{PQ}=\frac{2}{3}Mr^2+Mr^2\\or,\ I_{PQ}=\frac{5}{3}Mr^2 \)