(i) Moment of inertia of a hollow sphere about a diameter:

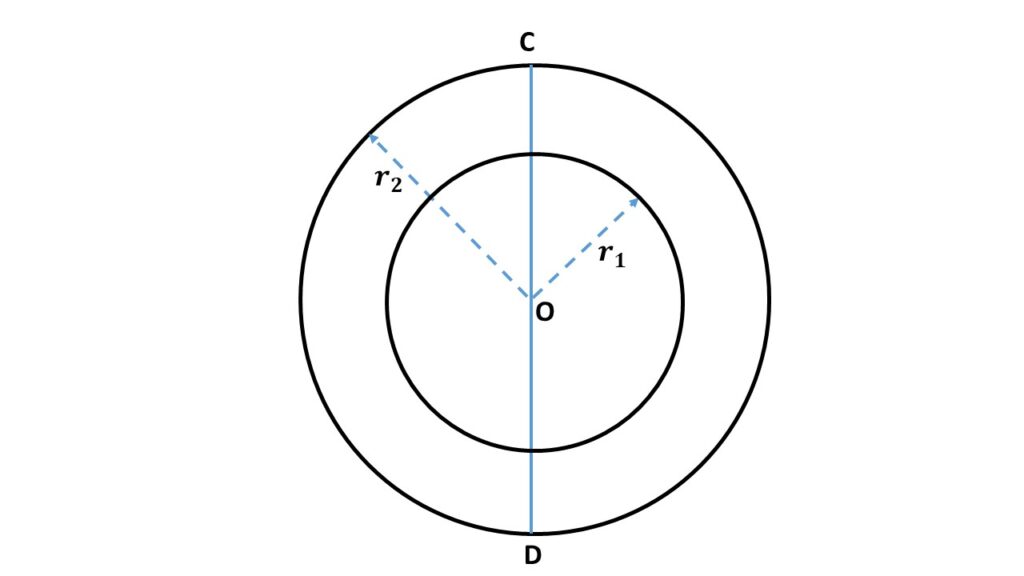
Let us consider a hollow sphere of inner radius \( r_1 \) and outer radius \( r_2 \). So the volume of this hollow sphere is \( \frac{4}{3}\pi(r_2^3-r_1^3) \). If M be the mass of the hollow sphere, then mass density i.e., mass per unit volume of the hollow sphere is \( \frac{M}{\frac{4}{3}\pi(r_2^3-r_1^3)} \) = \( \frac{3M}{4\pi(r_2^3-r_1^3)} \).

In order to calculate the moment of inertia of this hollow sphere about the diameter CD, we can assume two concentric spheres, one of radius \( r_1 \) and the other is of radius \( r_2 \). The mass of the sphere of radius \( r_1 \) is \( M_1=\frac{4}{3}\pi{r_1}^3\times{\frac{3M}{4\pi(r_2^3-r_1^3)}} \) = \( \frac{M{r_1}^3}{(r_2^3-r_1^3)} \). The mass of the sphere of radius \( r_2 \) is \( M_2=\frac{4}{3}\pi{r_2}^3\times{\frac{3M}{4\pi(r_2^3-r_1^3)}} \) = \( \frac{M{r_2}^3}{(r_2^3-r_1^3)} \).

The moment of inertia of the sphere of radius \( r_1 \) about the diameter CD is
\( I_1=\frac{2}{5}M_1{r_1}^2\\=\frac{2}{5}\frac{M{r_1}^3}{(r_2^3-r_1^3)}{r_1}^2\\=\frac{2}{5}\frac{M{r_1}^5}{(r_2^3-r_1^3)} \)

[ To know the derivation of the moment of inertia of a solid sphere about its diameter Click Here.]

The moment of inertia of the sphere of radius \( r_2 \) about the diameter CD is,

\( I_2=\frac{2}{5}M_2{r_2}^2\\=\frac{2}{5}\frac{M{r_2}^3}{(r_2^3-r_1^3)}{r_2}^2\\=\frac{2}{5}\frac{M{r_2}^5}{(r_2^3-r_1^3)} \)

So the moment of inertia of the hollow sphere about the diameter CD is ,
\( \displaystyle{I=I_2-I_1\\or,\ I=\frac{2}{5}\frac{(r_2^5-r_1^5)}{(r_2^3-r_1^3)}} \)

(ii) Moment of inertia of a hollow sphere about its tangent:

By applying theorem of parallel axes, we can calculate the moment of inertia of the hollow sphere about a tangent EF, which is parallel to the axis CD, and the perpendicular distance between these two axes CD and EF is \( r_2 \).

Therefore the moment of inertia of the hollow sphere about the axis EF is

\( I_{EF}=I+Mr_2^2 \)

or, \( \displaystyle{I_{EF}=\frac{2}{5}\frac{(r_2^5-r_1^5)}{(r_2^3-r_1^3)}+Mr_2^2} \)

(iii) The moment of inertia of the hollow sphere about its centre:

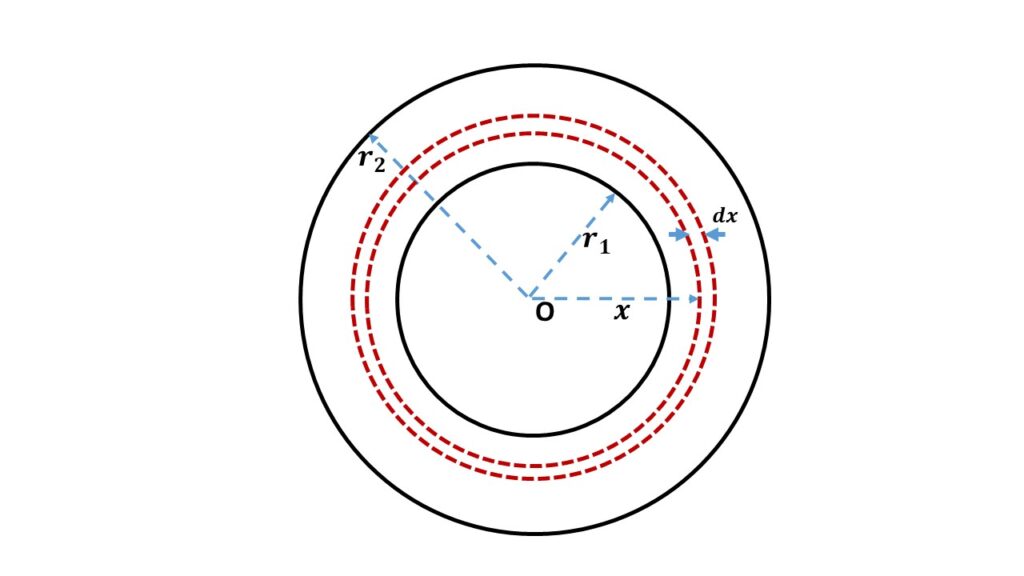
Let us consider a hollow sphere of inner radius \( r_1 \) and outer radius \( r_2 \).So the volume of the sphere is \( \frac{4}{3}\pi(r_2^3-r_1^3) \). If M be the mass of this hollow sphere, then the mass density i.e., mass per unit volume of this hollow sphere is \( \frac{M}{\frac{4}{3}\pi(r_2^3-r_1^3)} \) = \( \frac{3M}{4\pi(r_2^3-r_1^3)} \).

In order to calculate the moment of inertia of this hollow sphere about the centre O, let us consider an elementary concentric spherical shell of radius \( x \) and thickness \( dx \) with centre at O.

So the volume of this shell is \( 4\pi{x^2}dx \) and the mass is \( 4\pi{x^2}dx\times{\frac{3M}{4\pi(r_2^3-r_1^3)}} \) = \( \frac{3M}{r_2^3-r_1^3}x^2{dx} \).

The moment of inertia of this elementary shell about the centre O is \( \frac{3M}{r_2^3-r_1^3}x^2{dx}\times{x^2} \) = \( \frac{3M}{r_2^3-r_1^3}x^4{dx} \)

Now the moment of inertia of the whole hollow sphere about the centre \( O \) is given by,

\( I_0=\displaystyle{\int_{r_1}^{r_2}}\frac{3M}{r_2^3-r_1^3}x^4{dx}\\=\frac{3M}{5(r_2^3-r_1^3)}{\left(x^5\right)}_{r_1}^{r_2} \)

or, \( \displaystyle{I_0=\frac{3}{5}M\frac{(r_2^5-r_1^5)}{(r_2^3-r_1^3)}} \)