Range of Flow:
As the liquid escapes through the orifice, it has zero vertical velocity and let \( v \) be the horizontal velocity. It flows out in the form of a parabolic jet. Let this jet strikes the ground at a distance s from the tank after a time \( t \).
Let \( h_1 \)be the vertical distance covered by the jet in time \( t \).
\( h_1=(0\times{t})+\frac{1}{2}gt^2 = \frac{1}{2}gt^2 \)or, \( t=\sqrt{\frac{2h_1}{g}} \)
So the horizontal distance covered by the jet or the range of the liquid flow is,
\( S=vt=\sqrt{2gh}\times\sqrt{\frac{2h_1}{g}} \)To find the value of \( v \), READ THIS
or, \( S=2\sqrt{hh_1} \)
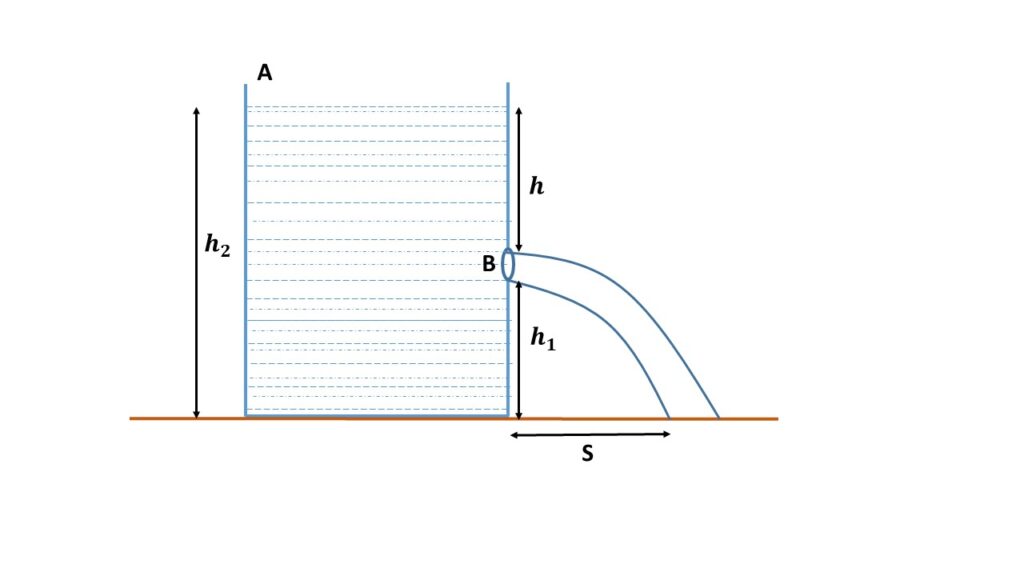
or, \( S^2=4hh_1=4h(h_2-h_1) \)
or, \( S^2=4(hh_2-h^2)=f(h) \)
Differentiating both side ,
\( 2S\frac{dS}{dh}=4(h_2-2h) \)or, \( S\frac{dS}{dh}=2(h_2-2h) \)
For maximum horizontal range \( \frac{dS}{dh}=0 \)
so, \( 2(h_2-2h)=0\\0r,\ h_2=2h \)
or, \(\displaystyle{ h=\frac{h_2}{2}} \)
Therefore for the range of the liquid to be maximum, the orific must be at the height which is half the height of the liquid column.