Gravitational potential at a point on the axis of a homogeneous cylinder:
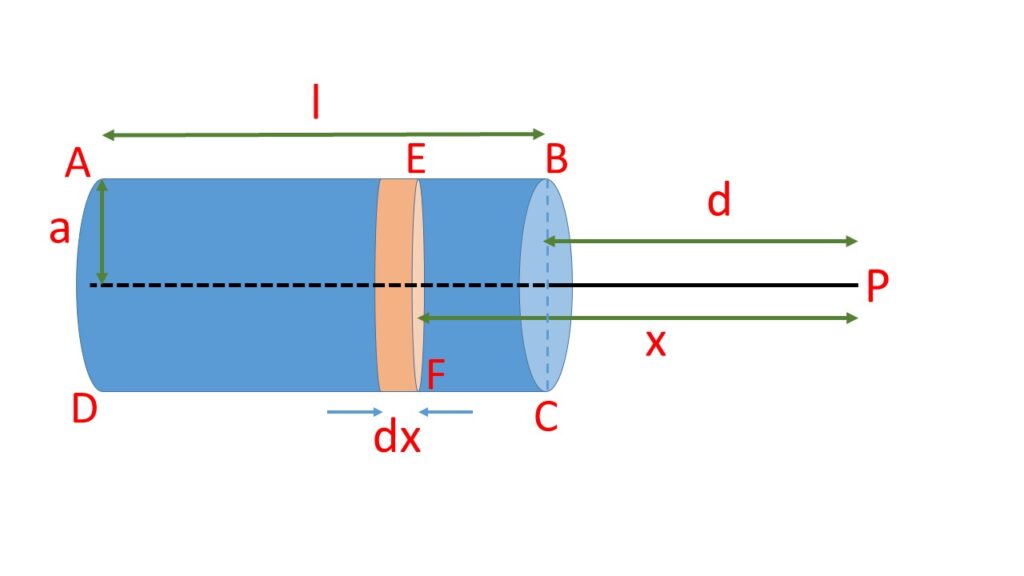
Let us consider a solid homogeneous cylinder \( ABCD \) of radius \( a \), length \( l \) and uniform mass density \( \rho \). There is a point \( P \) on the axis of the cylinder at a distance \( d \) from the face \( BC \) of the cylinder. We want to calculate the gravitational potential and gravitational intensity at the point \( P \) due to the cylinder.
In order to do that let us divide the cylinder into a number of co-axial discs. There is one such disc \( EF \) of thickness \( dx \), at a distance \( x \) from the point \( P \), as shown in the adjoining Fig. 1.
Hence the gravitational potential at \( P \) due to the disc \( EF \) is given by,
\( dv=2\pi\rho{G}\left[x-\sqrt{x^2+a^2}\right]\cdot{\,dx} \),
We can write the above expression with the help of the expression for potential due to a disc,READ IN DETAIL
Therefore the gravitational potential due to the entire cylinder at the point \( P \) is given by,
\( V=2\pi\rho{G}\displaystyle\int_{x=d}^{x=d+l}(x-\sqrt{x^2+a^2})\cdot{\,dx} \)= \( 2\pi\rho{G}[\frac{x^2}{2}|_d^{d+l}-\int_d^{d+l}\sqrt{x^2+a^2}dx] \)
= \( 2\pi\rho{G}\left[\frac{x^2}{2}-\frac{x\sqrt{x^2+a^2}}{2}\\-\frac{a^2}{2}{log}(x+\sqrt{x^2+a^2})\right]_d^{d+l} \)
= \( \pi\rho{G} \left[{x^2}-{x\sqrt{x^2+a^2}} \\ -{a^2}{log}(x+\sqrt{x^2+a^2})\right]_d^{d+l} \)
= \( \pi\rho{G}\left[ l(l+2d)-(d+l)\sqrt{(d+l)^2+a^2} \\+d\sqrt{d^2+a^2} \\-a^2{log}((d+l)\sqrt{(d+l)^2+a^2}) \\+a^2{log}(d+\sqrt{d^2+a^2}) \right] \)
= \( \pi\rho{G} \left[ l(l+2d)-(d+l)\sqrt{(d+l)^2+a^2} \\+d\sqrt{d^2+a^2} \\-a^2{log} \frac{ ((d+l)\sqrt{(d+l)^2+a^2}) }{ (d+\sqrt{d^2+a^2}) } \right] \)
= \( \frac{GM}{la^2}\left[ l(l+2d)-(d+l)\sqrt{(d+l)^2+a^2} \\+d\sqrt{d^2+a^2} \\-a^2{log} \frac{ ((d+l)\sqrt{(d+l)^2+a^2}) }{ (d+\sqrt{d^2+a^2}) } \right] \)
where \( M=\pi{a^2}l\rho \) is the total mass of the cylinder.
Again attraction at a point \( P \) due to the elementary disk \( EF \) is given by,
\( dE=2\pi\rho{G}\left[1-\frac{x}{\sqrt{x^2+a^2}}\right]\cdot\,dx \).
Hence the resultant attraction at \( P \) due to the entire cylinder is,
\( E=2\pi\rho{G}\displaystyle\int_d^{d+l} \left[1-\frac{x}{\sqrt{x^2+a^2}}\right]\cdot\,dx \)= \( 2\pi{G}\rho\left[x-\sqrt{x^2+a^2}\right]_d^{d+l} \)
= \( 2\pi{G}\rho\left[l-\sqrt{({d+l}^2)+a^2} \\+\sqrt{({d^2+a^2})}\right] \)
= \( \frac{2GM}{la^2} \left[l-\sqrt{({d+l}^2)+a^2} \\+\sqrt{({d^2+a^2})}\right] \)
where \( M=\pi{a^2}l\rho \) is the total mass of th ecylinder.
Solution of \( \displaystyle\int\frac{x}{\sqrt{x^2+a^2}}\cdot\,dx \):
put, \( x^2+a^2=z^2 \ or,\ x\,dx=z\,dz \)
\( \displaystyle\int\frac{x}{\sqrt{x^2+a^2}}\cdot\,dx \\=\displaystyle\int\frac{z\,dz}{z} \\=\displaystyle\int\,dz\\=z =\sqrt{x^2+a^2} \)