Ans.

A particle is dropped vertically on a fixed horizontal plane from a height \( H \) above the plane.
At height \( H \) the particle is at rest, i.e., the initial velocity of the particle is zero.

Let \( u \) be the velocity of the particle just before the collision with the plane and \( v \) be the velocity just after the particle hits the plane, as shown in the Fig. 1

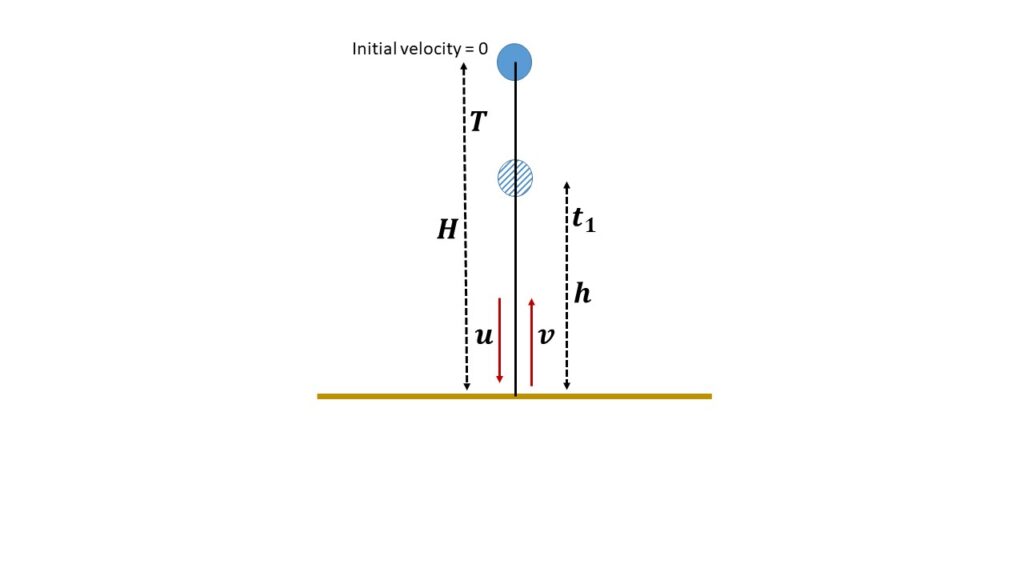
Let \( T \) be the time taken by the particle to cover the height \( H \) just before the 1st collision with the plane, then

\( u=0+gT \)

or, \( u=gT \)

where, \( g \) is the acceleration due to gravity.

Let, \( t_1 \) be the time taken by the particle after 1st collision to reach the height \( h \), then

\( 0=v-gt_1 \)

or, \( v=gt_1 \)

If \( e \) be the coefficient of restitution, then

\( e=\frac{v-0}{u-0} \)

or, \( e=\frac{v}{u} \)

or, \( e=\frac{gt_1}{gT} \)

or, \( e=\frac{t_1}{T} \)

or, \( t_1=eT \)

If \( t_2 \), \( t_3 \) and so on, be the time taken by the particle after 2nd collision, 3rd collision and so on respectively, then

\( t_2=et_1=e\cdot{eT}=e^2T \),

\( t_3=e\cdot{t_2}=e^3T \),

and so on \( \cdots \)

So the total theoretical time taken by the particle to come to rest is

\( T+2t_1+2t_2+2t_3+\cdots \)

=\( (2T+2t_1+2t_2+2t_3+\cdots)-T \)

= \( (2T+2eT+2e^2T+2e^3T+\cdots)-T \)

= \( 2T(1+e+e^2+e^3+\cdots)-T \)

= \( \displaystyle{2T\frac{1}{1-e}-T} \)

= \( \displaystyle{T\frac{2-1+e}{1-e}} \)

= \( \displaystyle{T\frac{1+e}{1-e}} \)

Again, \( H=0\cdot{T}+\frac{1}{2}gT^2 \)

or, \( \displaystyle{T=\sqrt{\frac{2H}{g}}} \)

Therefore, the total theoretical time taken by the particle to come to rest is

\( \displaystyle{\sqrt{\frac{2H}{g}}\cdot{\frac{1+e}{1-e}}} \)