Ans.

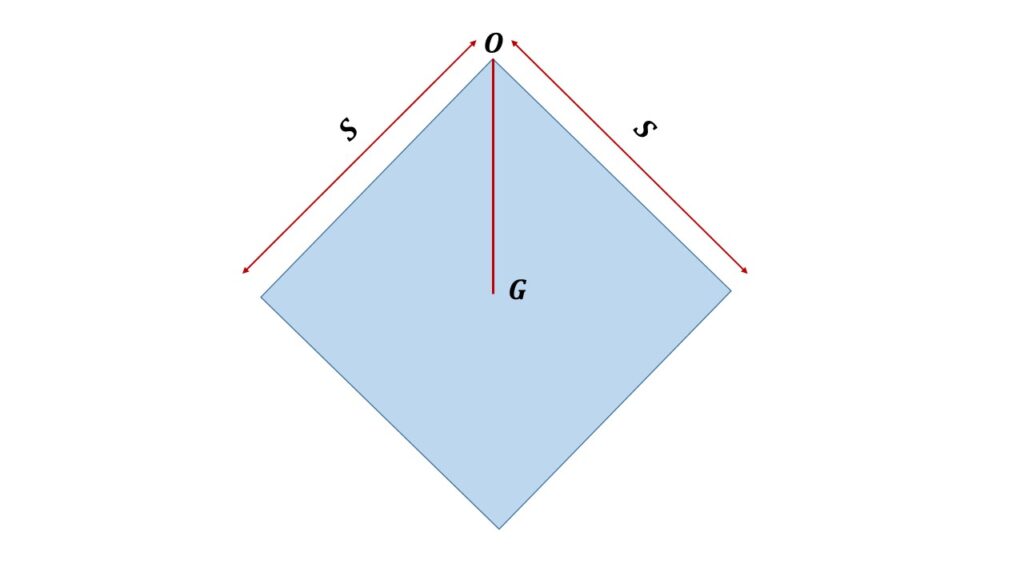
Let us consider a cube of mass \( M \) and edges \( S \) is suspended from one of its edges O as shown in the Fig. 1.

The length of the diagonal of the cube of edges \( S \) is

\( \sqrt{S^2+S^2+S^2}=\sqrt{3}S \)

If \( G \) be the centre of gravity of the cube of side S, then \( OG=\frac{\sqrt{3}}{2}S \).

The moment of inertia of the cube about an edge is the same as the moment of inertia of a square plate of same length of side about a side.

If M be the mass of the cube then the moment of inertia of the cube is

\( I=\frac{1}{3}M\left(S^2+S^2\right) \)

or, \( I=\frac{2}{3}MS^2 \)

Therefore the time period of oscillation of the cube is

\( \displaystyle{T=2\pi\sqrt{\frac{\frac{2}{3}MS^2}{\frac{\sqrt{3}}{2}S}}} \)

or, \( \displaystyle{T=2\pi\sqrt{\frac{4}{3\sqrt{3}}\frac{S}{g}}} \)

Let L be the length of the equivalent simple pendulum, then the time period of oscillation of that equivalent simple pendulum is

\( \displaystyle{T=2\pi\sqrt{\frac{L}{g}}} \)

or, \( \displaystyle{L=\frac{g}{4{\pi}^2}T^2} \)

or, \( \displaystyle{L=\frac{g}{4{\pi}^2}4{\pi}^2\frac{4}{3\sqrt{3}}\frac{S}{g}} \)

or, \( \displaystyle{L=\frac{4}{3\sqrt{3}}S} \)