Venturimeter:

Venturimeter is a device to measure the rate of flow of a liquid through a pipe based on Bernoulli’s theorem, as shown in Fig.1. It consists of a horizontal pipe whose middle portion is narrow and two sides are wide.

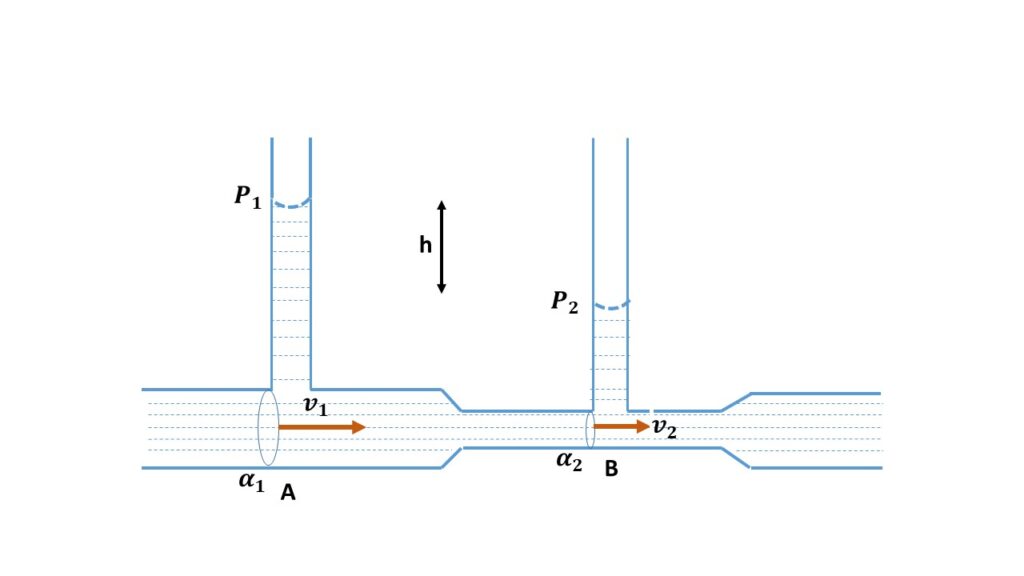
Let us consider \( P_1 \) and \( v_1 \) be the pressure and velocity of the liquid at the point \( A \). \( P_2 \) and \( v_2 \) are the pressure and velocity respectively at the point \( B \). Let \( \rho \) be the density of the liquid.

According to Bernoulli’s theorem,

\( \frac{{v_1}^2}{2}+\frac{P_1}{\rho}=\frac{{v_2}^2}{2}+\frac{P_2}{\rho} \)

[Since the tube is horizontal, so the elevation heads at A and B are equal.]

or, \( \frac{(P_1-P_2)}{\rho}=\frac{{v_2}^2-{v_1}^2}{2} \)

or, \( \frac{h\rho{g}}{\rho}= \frac{{v_2}^2-{v_1}^2}{2} \)

[where, \( (P_1-P_2)=h\rho{g} \), \( h \) is the difference of heights of the liquid columns at the vertical tubes attached to the venturimeter.]

or, \( \displaystyle{h=\frac{{v_2}^2-{v_1}^2}{2g}} \)

If \( \alpha_1 \) and \( \alpha_2 \) be the cross sectional areas at \( A \) and \( B \) respectively then from equation of continuity, we get

\( \alpha_1v_1=\alpha_2v_2 \\or,\ \frac{v_2}{v_1}=\frac{\alpha_1}{\alpha_2} \)

Or, \( \displaystyle{h=\frac{{v_1}^2}{2g}(\frac{{v_2}^2}{{v_1}^2}-1) \\= \frac{{v_1}^2}{2g}(\frac{\alpha_1^2}{\alpha_2^2}-1)} \)

or, \( \displaystyle{h=\frac{{v_1}^2}{2g}\frac{\alpha_1^2-\alpha_2^2}{\alpha_2^2}} \)

or, \( \displaystyle{v_1=\frac{\alpha_2}{\sqrt{\alpha_1^2-\alpha_2^2}}\sqrt{2gh}} \)

Rate of flow of liquid is,

\( \displaystyle{V=\alpha_1v_1=\alpha_1\alpha_2\sqrt{\frac{2gh}{\alpha_1^2-\alpha_2^2}}} \)