Torricelli’s Theorem:

This theorem states that the velocity of efflux of a liquid through an orifice is equal to the velocity which a freely falling body attains while falling through a height equal to the height of the free surface of the liquid above the orifice.

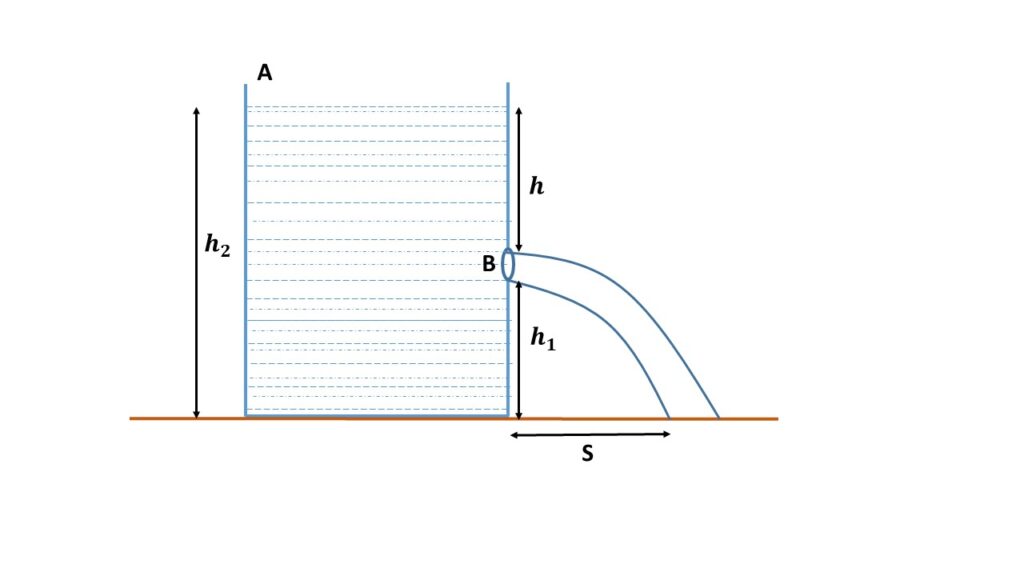
Velocity of Efflux of a liquid:

Let us consider a liquid contained in a tank with a free surface at \( A \) and with a narrow orifice at \( B \). Let \( \rho \) be the density of the liquid. Let \( h_2 \) be the total depth of the liquid, \( h \) be the height of the liquid surface above \( B \). \( h_1 \) be the height of the orifice above the bottom of the tank. Let \( v \) be the velocity of discharge of the liquid through the orifice \( B \). Let \( P \) be the pressure, which is atmospheric pressure, at both ends \( A \) and \( B \). As the tank has a large diameter and the orifice is small, it may be assumed that the height of the liquid at the free surface decreases very slowly. So the velocity of the liquid at the free surface may be assumed to be zero. Considering a flow tube of different cross-sections, starting from the free surface \( A \) of the tank and ending at the orifice \( B \), applying Bernoulli’s theorem we can write,

\( \frac{P}{\rho}+0+g{h_2}=\frac{P}{\rho}+\frac{1}{2}v^2+g{h_1} \)

where, \( g \) is the acceleration due to gravity

or, \( g{h_2}=\frac{1}{2}v^2+g{h_1} \)

or, \( \frac{1}{2}v^2=g(h_2-h_1) \)

or, \( v=\sqrt{2g(h_2-h_1)} \)

or, \( v=\sqrt{2gh} \)

where, \( (h_2-h_1)=h \)

This is known as the velocity of efflux.