Gravitational potential and intensity due to a hollow sphere:
(i) At a point \( P \) outside the hollow sphere:
Let us consider a hollow sphere of inner radius \( b \) and outer radius \( a \) (where \( a \) > \( b \) ) of mass \( M \) and density \( \rho \). Now consider a point \( P \) at a distance \( r \) from the centre \( O \) of the hollow sphere. We are going to calculate the gravitational potential and gravitational intensity at the point \( P \) due to the hollow sphere.
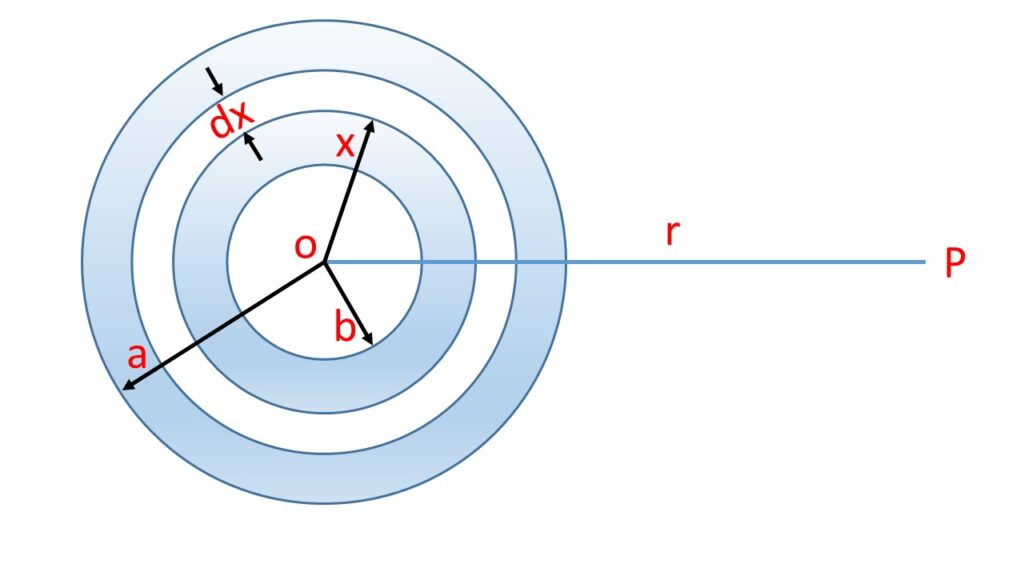
Let us consider a thin spherical shell of radius \( x \) and thickness \( \,dx \) with centre at the point \( O \) as shown in the above Fig. 1
Now the potential at \( P \), due to this thin spherical shell is
\( \,dv=-G\frac{4\pi{x^2}\,dx\cdot{\rho}}{r} \\=-\frac{4\pi{rho}G}{r}{x^2}\,dx \)Where the mass of the spherical shell of radius \( x \) and thickness \( \,dx \) is \( 4\pi{x^2}\,dx\rho \). Here it is considered that the mass is concentrated at the centre.
The potential at \( P \) due to this hollow sphere of radii \( a \) and \( b \) is
\( V=\displaystyle\int_b^a\,dv=-\frac{4\pi\rho{G}}{r}\displaystyle\int_b^a{x^2}\,dx \\=- \frac{4\pi\rho{G}}{3r}(a^3-b^3) \\=-\frac{4}{3}\pi(a^3-b^3)\rho\frac{G}{r} \\=-\frac{GM}{r} \)where, \( \frac{4}{3}\pi(a^3-b^3)\rho = M \) is the total mass of the hollow sphere.
Now, Gravitational Intensity at \( P \) is
\( E=-\frac{\,dv}{\,dr} \\=-\frac{d}{\,dr}( -\frac{4}{3}\pi(a^3-b^3)\rho\frac{G}{r}) \\=G\frac{4}{3}\pi(a^3-b^3)\rho\frac{d}{\,dr}(\frac{1}{r}) \\=-G \frac{4}{3}\pi(a^3-b^3)\rho \cdot\frac{1}{r^2} \\or,\ E=-\frac{GM}{r^2} \)where, \( M= \frac{4}{3}\pi(a^3-b^3)\rho \) is the mass of the sollow sphere.
(ii) At a point \( P \) inside a hollow sphere:
Let us consider a point \( P \) inside the hollow sphere at a distance \( r \) from the centre \( O \).
Let’s consider the thin spherical shell of radius \( x \) and thickness \( dx \) with the centre at \( O \), as shown in the adjoining Fig. 2.
The mas of that thin spherical shell is \( 4\pi{x^2}\,dx\rho \). now the potential at P due to this spherical shell is,
\( dv=-G \frac{ 4\pi{x^2}\,dx\rho }{x} \\=-4\pi{G}\rho\cdot{x\,dx} \)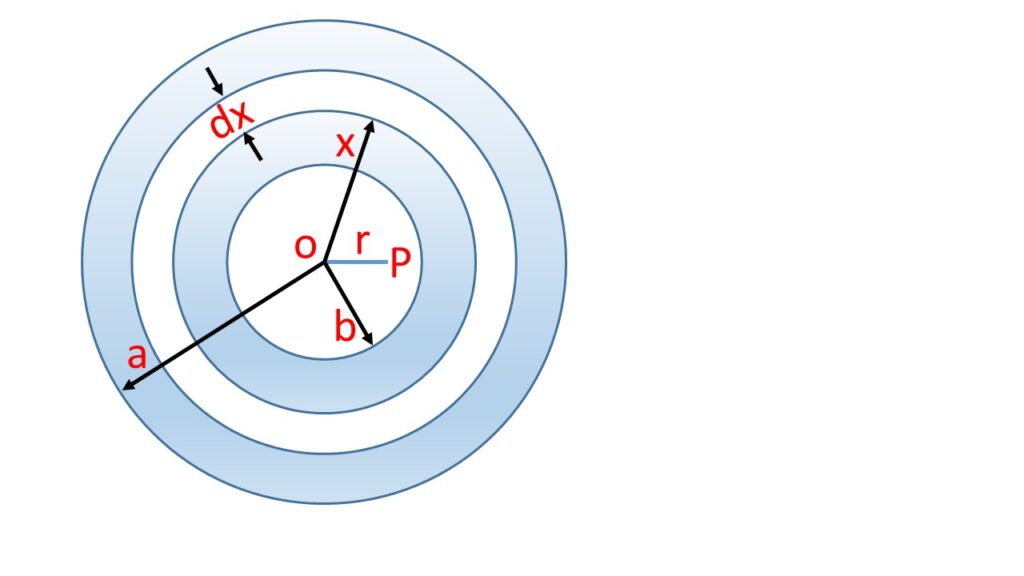
We know that the gravitational potential inside the shell is the same as on the surface. [READ IN DETAIL]
Gravitational potential at \( P \) due to the whole hollow sphere of inner radius \( b \) and outer radius \( a \) is given by,
\( V=\displaystyle\int_b^a\,dv \\=-G4\pi\rho\displaystyle\int_b^ax\,dx \\=-G2\pi\rho(a^2-b^2) \\=-G\frac{4}{3}\pi(a^3-b^3)\rho\frac{3(a^2-b^2)}{2(a^3-b^3)} \\=-\frac{3}{2}GM\left(\frac{a^2-b^2}{a^3-b^3}\right) \)Here the total mass of the hollow sphere is \( M=\frac{4}{3}\pi(a^3-b^3)\rho \).
Now the gravitational intensity at \( P \) is ,
\( E=-\frac{\,dv}[{\,dr} \\=-\frac{d}{\,dr}\left[-\frac{3}{2}GM\frac{a^2-b^2}{a^3-b^3}\right] \\=0 \)(iii) At a point \( P \) inside the material of the hollow sphere:
Let us consider a point \( P \) at a distance \( r \) inside the material of the hollow sphere of inner radius \( b \) and outer radius \( a \), where \( b<r<a \).
Now consider a sphere of radius \( r \) with \( O \) at the centre.
As the point \( P \) lies just inside the spherical shell of inner radius \( r \) and outer radius \( a \)., then the gravitational potential at \( P \) is \( V_1=-2\pi\rho{G}(a^2-r^2) \).
Again the point \( P \) just lies on the surface of the spherical shell of the inner radius \( b \) and outer radius \( r \). Now the gravitational potential at \( P \) is \( V_2=-\frac{4}{3}G\pi\frac{(r^3-b^3)}{r}\rho \).
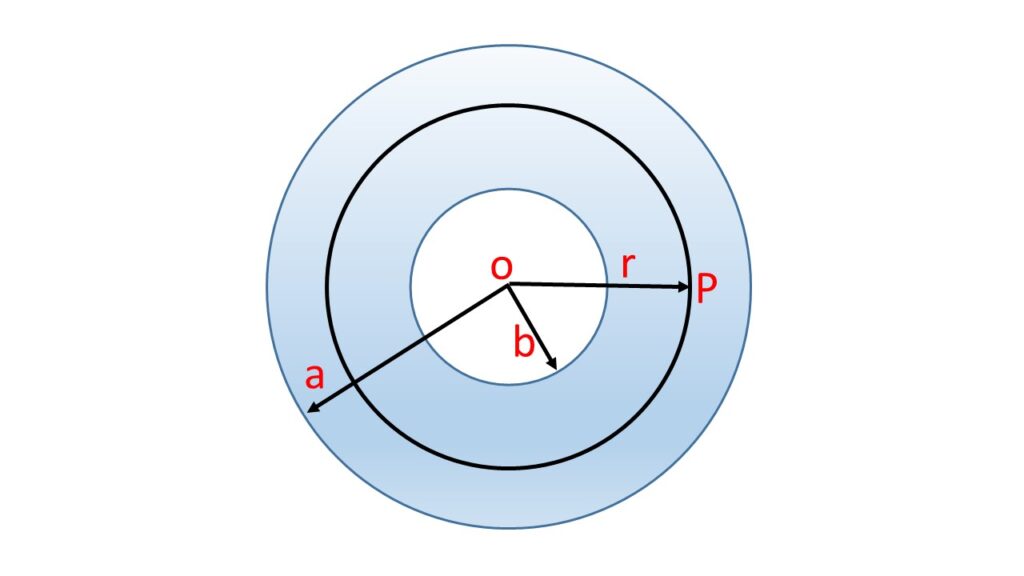
Now the total potential at \( P \) is \( V=V_1+V_2 \\=-[ 2\pi\rho{G}(a^2-r^2) + \frac{4}{3}G\pi\frac{(r^3-b^3)}{r}\rho ] \\= -2\pi\rho{G}(a^2-r^2+\frac{2}{3}r^2-\frac{2}{3}\frac{b^3}{r}) \)
\( or,\ V=-2\pi\rho{G}(a^2-\frac{1}{3}r^2- \frac{2}{3}\frac{b^3}{r}) \)Now, gravitational potential at the point \( P \) is,
\( E=-\frac{\,dv}{\,dr} \\= 2\pi\rho{G} \frac{d}{\,dr}\left(a^2-\frac{1}{3}r^2- \frac{2}{3}\frac{b^3}{r}\right) \\= 2\pi\rho{G} \left(-\frac{2}{3}r+\frac{2b^3}{3r^2}\right) \\=\frac{4}{3}\pi\rho{G}\left(-r+\frac{b^3}{r^2}\right) \\or,\ E=-\frac{4\pi\rho{G}}{3r^2}\left(r^3-b^3\right) \)