Gravitational potential due to a homogeneous solid sphere:
The amount of work done in bringing a unit mass from infinity to any point in the gravitational field is called the gravitational potential at that point. READ IN DETAILS
(i) When the point \( P \) is ouside the sphere:
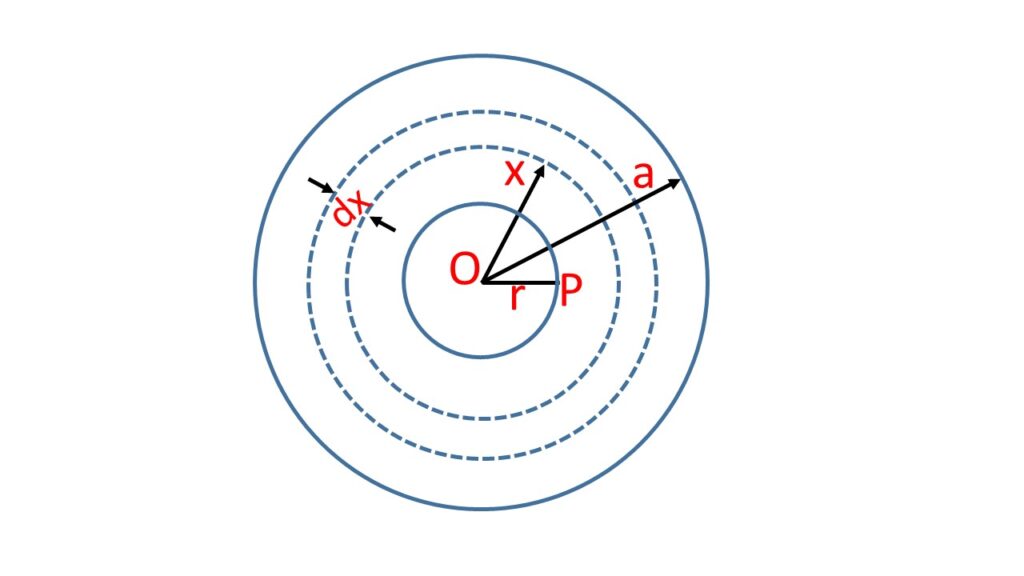
Let us consider a solid sphere of radius \( a \) and mass \( M \). Let us consider a point \( P \) at a distance \( r \) from the centre \( O \) of the sphere. We want to calculate the gravitational potential at the point \( P \)
Let us consider a thin spherical shell of radius \( x \) and thickness \( dx \)

Now the mass of this selected spherical shell is \( 4\pi{x}^2\,dx\rho \), where \( \rho \) is the mass density of the shere.
The potential at \( P \), due to this thin spherical shell is
\( \,dv=-\frac{G( 4\pi{x}^2\,dx\rho )}{r} \).
Total potential at \( P \) due to this whole solid sphere is,
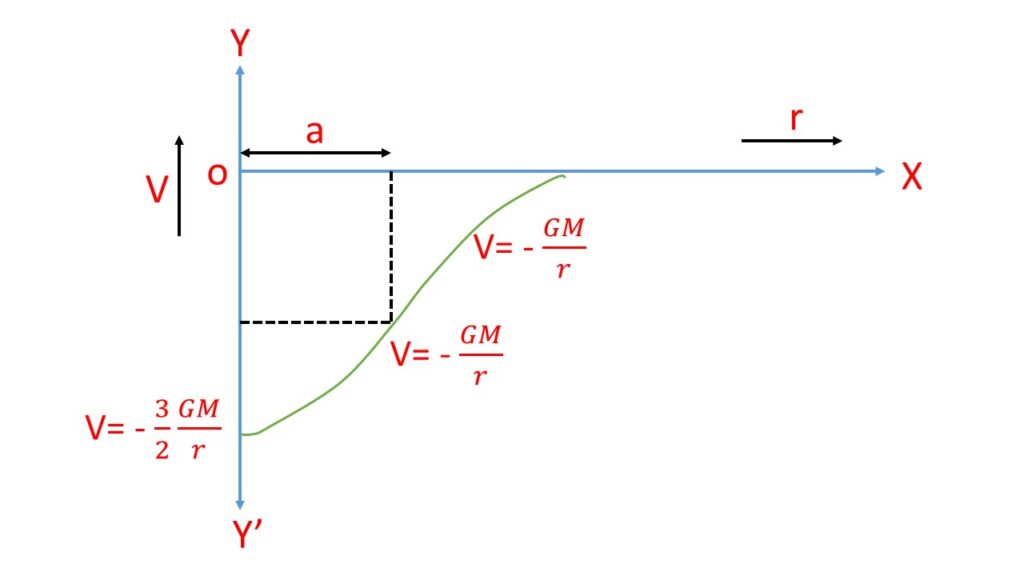
\( V=-\frac{G4\pi\rho}{r}\displaystyle\int_{0}^{x^2}\,dx = -G\frac{4\pi\rho}{r}\frac{a^3}{3} \\ =-G\frac{4\pi{a^3}\rho}{3r}\) \( \displaystyle{V=-\left(\frac{GM}{r}\right)} \)where, \( M=\frac{4}{3}\pi{a^3}\rho \) is the total mass of the solid spherical shell.
Here for an external point, the solid sphere behaves as if its whole mass were concentrated at the centre of the shell.
(ii) When the point \( P \) is on the surface of the sphere:
For a point on the surface of the sphere of radius \( a \), \( r=a \),
\( \displaystyle{V=-\left(\frac{GM}{a}\right)} \)(iii) When the point \( P \) is inside the sphere:
Let us consider a solid sphere of radius \( a \) and at a point \( P \) at a distance r from the centre \( O \) of the sphere and inside the sphere i.e, (r<a). Lets calculate the potential at \( P \).
Let us draw a sphere of radius \( r \) and centre at \( O \). Then \( P \) lies on the solid sphere of radius \( r=OP \). P also lies inside the spherical shell of internal radius \( r \) and external radius \( a \).
Now the potential at \( P \) due to the inner solid sphere of radius \( r \) is
\( V_1=-\frac{G(\frac{4}{3}\pi{r^3}\rho)}{r}=-\frac{4}{3}\pi{r^2}\rho{G} \)where, \( \rho \) is the mass density of the sphere and \( \frac{4}{3}\pi{r^3}\rho \) is the mass of the sphere of radius \( r \).
Lets find the potential at \( P \) due to the outer spherical shell of inner radius \( r \) and outer radius \( a \). To find this, lets draw a thin spherical shell of radius \( x \) and thickness \( \,dx \).
Now, we know that the potential at any point inside the spherical shell is the same as on the surface.
So we can write the potential at any point \( P \) due to this elementary spherical shell is
\( \,dv_2=-G\frac{4\pi{x^2}\,dx\cdot\rho}{x}\\=-4\pi{G}\rho{x}\cdot\,dx \)so the total potential at \( P \) due to the spherical shell of internal radius \( r \) and external radius \( a \) is
\( V_2=\displaystyle\int_r^a\,dv_2=-4\pi{G}\rho\displaystyle\int_r^ax\,dx \\=-2\pi{G}\rho(a^2-r^2)\)So the potential at \( P \) due to the whole sphere is
\( V=V_1+V_2 \\=-[\frac{4}{3}\pi{r^2}\rho{G}+2\pi{G}\rho(a^2-r^2)] \\=-2\pi\rho{G}[\frac{2}{3}{r^2}+a^2-r^2] \\=\frac{2}{3}\pi\rho{G}[3a^2-r^2] \\=-\frac{4}{3}\pi{a^3}\rho{G}\frac{3a^2-r^2}{2a^3} \)or, \( V=-GM\frac{3a^2-r^2}{2a^3} \)
where, \( M=\frac{4}{3}\pi{a^3}\rho \) is the mass of the solid sphere.
(iv) Potential at the centre of the sphere:
at the centre of the sphere is \( r=0 \).
\( V=-GM\frac{3a^2}{2a^3}=-\frac{3}{2}\frac{GM}{a} \)Graphical representation:
The variation of graphical potential due to a solid sphere is shown in the adjoining Fig. 3