(i)At a point outside the shell:

Gravitational potential at a point outside rthe thin uniform spherical shell, at a distance \( r \), \( (r>a) \) is given by, \( V=\displaystyle{-\frac{GM}{r}} \). Where \( G \) is the gravitational constant, \( M \) is the mass of the shell, \( a \) is the radius of the shell, \( r \) is the distance from the centre of the shell.

The Gravitational Potential Due To A Thin Uniform Spherical Shell At A Point (i)Outside, (ii)At The Surface, (iii) Inside The Shell. READ IN DETAILS

Gravitational intensity \( \displaystyle{E=-\frac{\,dv}{\,dr}=-\frac{d}{\,dr}(-\frac{GM}{r})\\ =GM\frac{d}{dr}(\frac{1}{r})} \)

or, \( \displaystyle{E=-\left(\frac{GM}{r^2}\right)} \)

Where the negative sign indicates that the \( E \) is always directed towards the centre O of the shell. Here the spherical shell behaves as if its whole mass are concentrated at the centre.

(ii) At a point on the surface of the shell:

The gravitational potential at a point on the surface of the shell of radius \( a \) and mas \( M \) is given by,

\( \displaystyle{V=-\frac{GM}{r}\vert_{at\ r=a}=-\frac{GM}{a}} \)

The gravitational intensity is

\( E=-\frac{\,dv}{\,dr}=-\frac{d}{\,dr}\left(-\frac{GM}{r}\right)_{r=a} \)

or, \( E=-\frac{GM}{a^2} \)

Here also the mass of the shell may be considered to be concentrated at the centre of the shell.

(iii) At a point inside the shell:

The gravitational potential at a point inside the spherical shell of radius \( a \) and mass \( M \) is given by,

\( V=-\left(\frac{GM}{a}\right) =\ constant \)

Gravitational intensity is given by,

\( E=-\frac{\,dv}{\,dr}=-\frac{d}{\,dr}\left(-\frac{GM}{a}\right)=0 \)

Here the gravitational intensity inside the shell is zero.

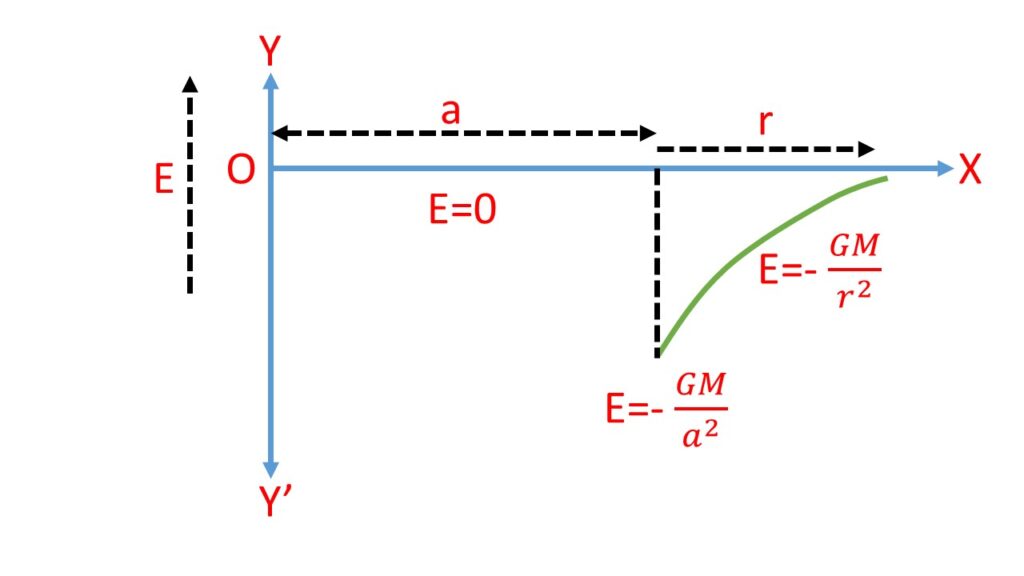
Graphical Representation: