Maxwell’s distribution law:
Maxwell’s distribution law is given by,
\(\displaystyle{n_i=\frac{g_i}{e^{\alpha+\frac{\epsilon_i}{kT}}}}\)
where, \(n_i\) is the number of the particles distributed in \(g_i\) states and \(\epsilon_{i}\) is the energy of each particle. \(\alpha\) is constant, \(k\) is Boltzmann constant and \(T\) is the absolute temperature.
Corroboration of Maxwell’s distribution law with the equipartition of energy:
Let us consider a continuous distribution of the molecular energies so that the energy levels are continuously distributed. The number of the molecules between the energy range \(\epsilon\) and \(\epsilon+d\epsilon\) is given by,
\(\displaystyle{n(\epsilon)\ d\epsilon=f(\epsilon)\ g(\epsilon)\ d\epsilon=\frac{g(\epsilon)\ d\epsilon}{e^{\alpha+\frac{\epsilon}{kT}}}}\tag{1}\)where, \(\displaystyle{f(\epsilon)=\frac{1}{e^{\alpha+\frac{\epsilon}{kT}}}}\) is the Maxwell-Boltzmann Distribution function.
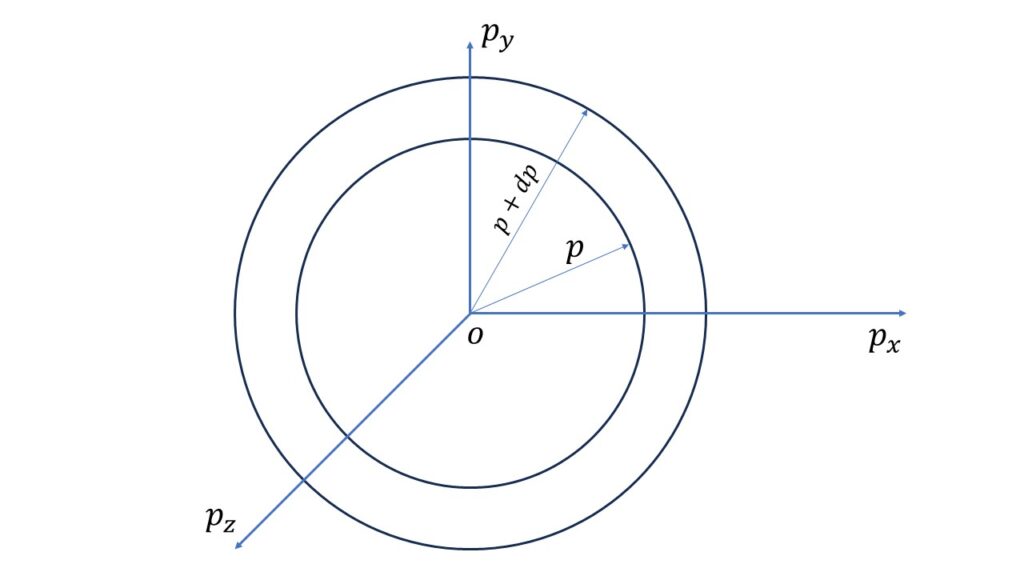
Now, the phase sphere volume in the momentum range \(p\) and \(p+dp\) is given by,
\(\displaystyle{\iiint}{dq_x}\cdot{dq_y}\cdot{dq_z}\ \displaystyle{\iiint_{p}^{p+dp}}{dp_x}\cdot{dp_y}\cdot{dp_z}\\=V\cdot{4\pi}p^2\ dp\)where, \(\displaystyle{\iiint}{dq_x}\cdot{dq_y}\cdot{dq_z}=V\), the co-ordinate volume.
So the number of the quantum states in the energy range \(\epsilon\) and \(\epsilon+d\epsilon\) is given by,
\(\displaystyle{g(\epsilon)\ d\epsilon=\frac{V\cdot{4\pi}p^2{dp}}{h^3}}\),
where \(h^3=dq_x\ dq_y\ dq_z\ \cdot\ dp_x\ dp_y\ dp_z\) is the volume of each quantum state.
\(\displaystyle{=\frac{4\pi{V}(\sqrt{2m\epsilon})^2\cdot\ d\sqrt{2m\epsilon}}{h^3}}\), where \(p=\sqrt{2m\epsilon}\)
\(\displaystyle{=\frac{4\pi{V}\cdot{2m\epsilon}\sqrt{2m}{\epsilon}^{-1/2}d\epsilon}{h^3}}\)
\(\displaystyle{=\frac{2\pi{V}{(2m)}^{3/2}{\epsilon}^{1/2}d\epsilon}{h^3}}\tag{2}\)Using (2) in (1) we get,
\(\displaystyle{n(\epsilon)\ d\epsilon=\frac{2\pi{V}{(2m)}^{3/2}{\epsilon}^{1/2}e^{-\alpha}e^{-\epsilon/kT}d\epsilon}{h^3}}\tag{3}\)In order to find the value of \(e^{-\alpha}\), we use the relation
\(N=\displaystyle{\int_{0}^{\infty}}n(\epsilon)\ d\epsilon\) \(\displaystyle{=\frac{4\pi{V}\cdot{2m}^{3/2}}{h^3}e^{-\alpha}\int_{0}^{\infty}{\epsilon}^{1/2}\cdot{e^{-\epsilon/kT}}\ d\epsilon}\) \(\displaystyle{=\frac{4\pi{V}\cdot{2m}^{3/2}}{h^3}e^{-\alpha}{(kT)}^{1/2}\cdot{kT}\cdot\int{x}^{1/2}\cdot{e}^{-x}\ dx}\)[putting \(\frac{\epsilon}{kT}=x,\ or,\ d\epsilon=kT\ dx\)]
\(\displaystyle{=\frac{4\pi{V}\cdot{2m}^{3/2}}{h^3}e^{-\alpha}{(kT)}^{3/2}\ \Gamma{(3/2)}}\) \(\displaystyle{=\frac{4\pi{V}\cdot{2m}^{3/2}}{h^3}e^{-\alpha}{(kT)}^{3/2}\frac{1}{2}\sqrt{\pi}}\) \(\displaystyle{=\frac{V\cdot{(2m\pi{kT})}^{3/2}\cdot{e^{-\alpha}}}{h^3}}\)Therefore, \(\displaystyle{e^{-\alpha}=\frac{Nh^3}{V}\frac{1}{{(2m\pi{kT})}^{3/2}}}\)
Now putting the value of \(e^{-\alpha}\) in equation (3) we get,
\(\displaystyle{n(\epsilon)\ d\epsilon=\frac{4\pi{V}\cdot{2m}^{3/2}}{h^3}\cdot{\frac{Nh^3}{V}\frac{1}{{(2m\pi{kT})}^{3/2}}}{\epsilon}^{1/2}e^{-\epsilon/kT}\ d\epsilon}\)
therefore,
\(\displaystyle{n(\epsilon)\ d\epsilon=2\pi{N}{\left(\frac{1}{\pi{kT}}\right)}^{3/2}{\epsilon}^{1/2}e^{-\epsilon/kT}\ d\epsilon}\tag{4}\)This is the Maxwell distribution law of energy giving the number of molecules having energy between \(\epsilon\) and \(\epsilon+d\epsilon\).
The total energy of the system is
\(\displaystyle{E=\int_{0}^{\infty}\epsilon\ n(\epsilon)\ d\epsilon}\) \(\displaystyle{=2\pi{N}{\left(\frac{1}{{\pi}kT}\right)}^{3/2}\int_{0}^{\infty}{\epsilon}^{3/2}e^{-\epsilon/kT}\ d\epsilon}\) \(\displaystyle{=2\pi{N}{\left(\frac{1}{{\pi}kT}\right)}^{3/2}{(kT)}^{1/2}\int_{0}^{\infty}x^{3/2}e^{-x}\ dx}\)[Putting \(\frac{\epsilon}{kT}=x\ or,\ d\epsilon=kT\ dx\)]
\(\displaystyle{=2\pi{N}{\left(\frac{1}{{\pi}kT}\right)}^{3/2}{(kT)}^{5/2}\ \Gamma\left(\frac{5}{2}\right)}\) \(\displaystyle{=2\pi{N}{\left(\frac{1}{{\pi}kT}\right)}^{3/2}{(kT)}^{5/2}\frac{3}{2}\cdot\frac{1}{2}\sqrt{\pi}}\)Therefore,
\(\displaystyle{E=\frac{3}{2}NkT}\)
The mean energy of a molecule is \(\displaystyle{u=\frac{E}{N}=\frac{3}{2}kT}\).
A molecule has three degrees of freedom. So the energy of a molecule per degree of freedom is \(\displaystyle{u_1=\frac{u}{3}=\frac{1}{2}kT}\).
This is the law of equipartition of energy.