The homogeneity of space indicates the translational invariance of the properties of the free space. Let us consider, the frames of reference S and S’ are taken in such a way that the Y and Z axes are parallel to each other and the origins O and O’ of the frames S and S’ respectively are displaced by a distance d along the x-axis. So in this case the experimental result performed in the S frame of reference will be the same as the experimental result of the same experiment performed in the S’ frame of reference. So the experimental result remains unchanged due to the displacement of the co-ordinates system.

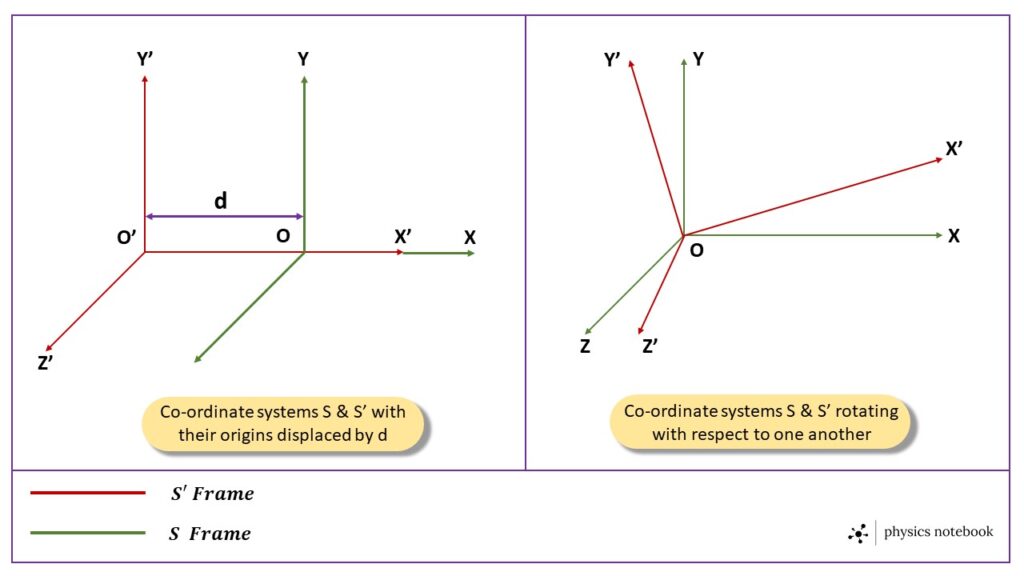
The isotropy of space indicates the rotational invariance of the free space. The rotational invariance means that, when the position co-ordinates of both the particles are rotated through some angle about an arbitrary axis, then the potential energy of interaction between the two particles remains unchanged. Let us consider two frames of reference S and S’, now they are rotating with respect to each other, then an experiment performed in the frame of reference S will give the same value when the same experiment is performed in the other frame of reference S’.