Ans.
Let us consider a solid circular cylinder of radius \( r \), length \( l \) and mass \( M \).
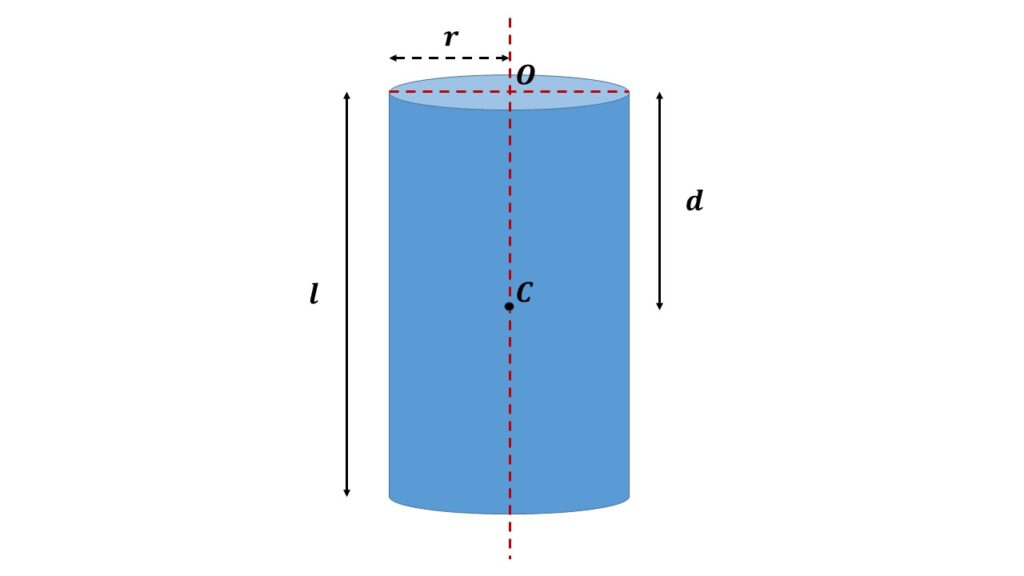
If \( I \) be the moment of inertia of the solid cylinder about an axis passing through the centre of gravity \( C \) and parallel to the axis of suspension through the centre of suspension \( O \), as shown in the Fig. 1, then
\( \displaystyle{I=M\left(\frac{l^2}{12}+\frac{r^2}{4}\right)} \)
[ to know the derivation of the above equation (CLICK HERE) ]
If \( K \) be the radius of gyration of the cylinder, then
\( I=MK^2 \)
or, \( \displaystyle{M\left(\frac{l^2}{12}+\frac{r^2}{4}\right)=MK^2} \)
or, \( \displaystyle{K^2=\left(\frac{l^2}{12}+\frac{r^2}{4}\right)} \)
The distance between the centre of suspension and centre of gravity is given, which is \( OC=d \),
If \( L \) be the length of the equivalent simple pendulum then,
\( \displaystyle{L=\frac{d^2+K^2}{d}} \)
or,\( \displaystyle{L=\frac{d^2+\left(\frac{l^2}{12}+\frac{r^2}{4}\right)}{d}} \)
or, \( \displaystyle{L=d+\frac{l^2+3r^2}{12d}} \)
So the time period of oscillation is
\( \displaystyle{T=2\pi\sqrt{\frac{L}{g}}} \)
or, \( \displaystyle{T=2\pi\sqrt{\frac{d+\left(\frac{l^2+3r^2}{12d}\right)}{g}}} \)
where \( g \) is the acceleration due to gravity
The time period of oscillation becomes minimum when, \( K^2=d^2 \)
\( \displaystyle{T_{min}=2\pi\sqrt{\frac{K^2+K^2}{Kg}}} \)
or, \( \displaystyle{T_{min}=2\pi\sqrt{\frac{2K}{g}}} \)
or, \( \displaystyle{T_{min}=2\pi\sqrt{\frac{2{\left(\frac{l^2+3r^2}{12}\right)}^{\frac{1}{2}}}{g}}} \)
or, \( \displaystyle{T_{min}=2\pi{\left(\frac{l^2+3r^2}{3g^2}\right)}^{\frac{1}{4}}} \)