Ans.

Let us consider a uniform solid sphere of radius \( a \) and of mass \( M \) is suspended vertically downward a from a point on its surface. G is the centre of gravity of the sphere.

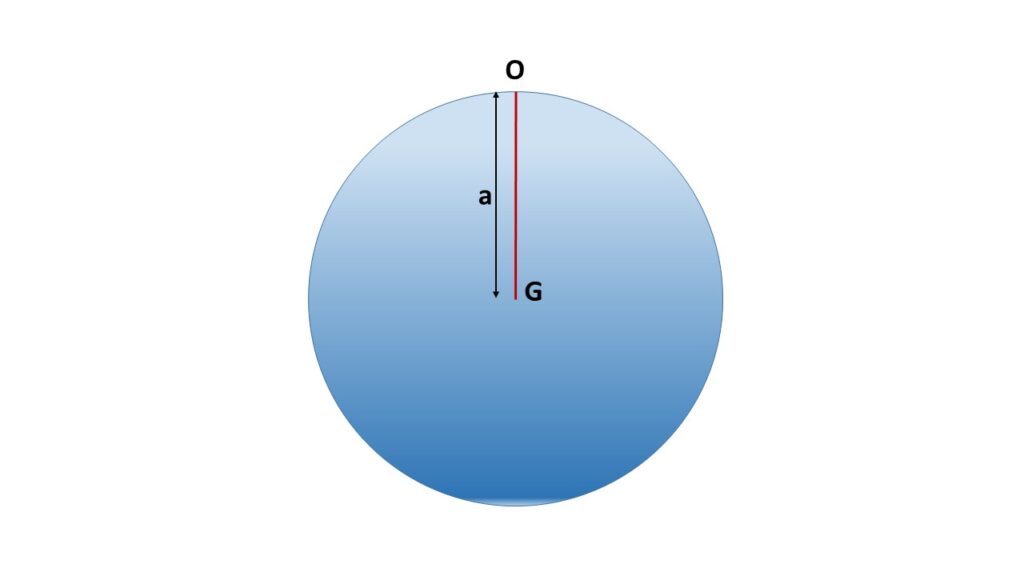
(i) Time period for small oscillation:

If \( I \) be the moment of inertia of this sphere about an axis passing through the point of suspension \( O \) perpendicular to the vertical plane, the

\( \displaystyle{I=\frac{7}{5}Ma^2} \)
[ to know the derivation of the above equation (CLICK HERE) ]

Again we know that the time period of oscillation is

\( \displaystyle{T=2\pi\sqrt{\frac{I}{Mga}}} \)
[ to know the derivation of the above equation (CLICK HERE) ]

where, g is the acceleration due to gravity.

or, \( \displaystyle{T=2\pi\sqrt{\frac{\frac{7}{5}Ma^2}{Mga}}} \)

or, \( \displaystyle{T=2\pi\sqrt{\frac{7a}{5g}}}\tag{1} \)

(ii) The length of the equivalent simple pendulum:

Let us consider the length of the equivalent simple pendulum of the solid sphere is

\( \displaystyle{T=2\pi\sqrt{\frac{L}{g}}} \)

Comparing this with equation (1), we get

\( \displaystyle{L=\frac{7a}{5}} \)