Ans.

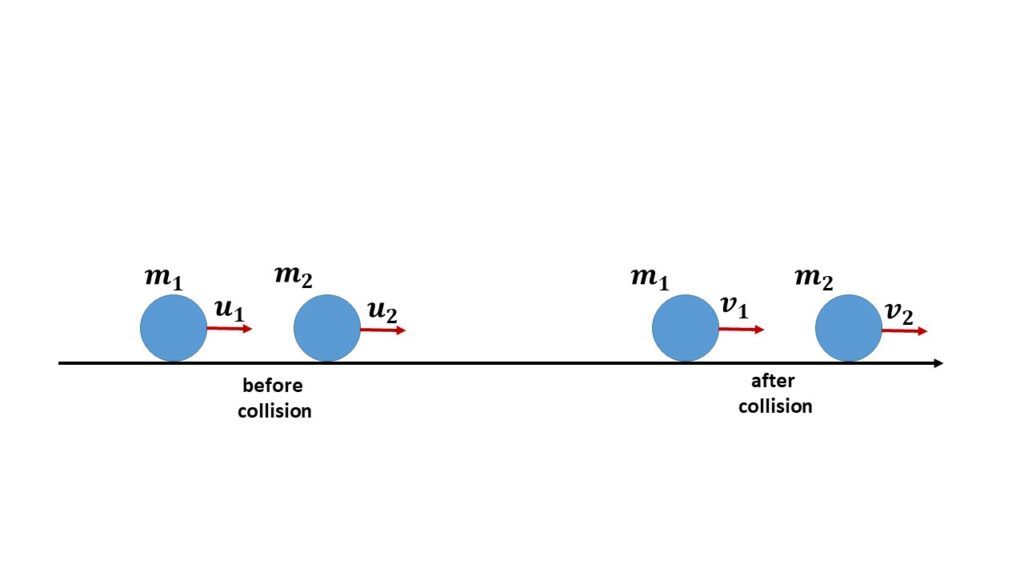
Let us consider, two particles of masses \( m_1 \) and \( m_2 \) travelling along the same straight line as shown in the fig.1. Let, \( u_1 \) and \( u_2 \) be their respective velocities before collision and \( v_1 \) and \( v_2 \) be their respective velocities after collision in the same direction of \( u_1 \) and \( u_2 \)

If \( e \) be the coefficient of restitution, then we can write

\( \displaystyle{e=\frac{v_2-v_1}{u_1-u_2}} \)

or, \( v_2-v_1=e(u_1-u_2)\tag{1} \)

According to the conservation of linear momentum,

total momentum before collision=total momentum after collision

or, \( m_1u_1+m_2u_2=m_1v_1+m_2v_2 \tag{2}\)

Multiplying equation (1) by \( m_2 \) and then substracting from equation (1), we get

\( (m_1v_1+m_2v_2)-(m_2v_2-m_2v_1)=(m_1u_1+m_2u_2)-em_2(u_1-u_2) \)

or, \( (m_1+m_2)v_1=(m_1-em_2)u_1+m_2(1+e)u_2 \)

or, \( \displaystyle{v_1=\frac{m_1-em_2}{m_1+m_2}u_1+\frac{m_2(1+e)}{m_1+m_2}u_2} \tag{3}\)

From equations (1) & (3), we get

\( v_2=v_1+e(u_1-u_2) \)

= \( \displaystyle{\frac{m_1-em_2}{m_1+m_2}u_1+\frac{m_2(1+e)}{m_1+m_2}u_2+e(u_1-u_2)} \)

= \( \displaystyle{(\frac{m_1-em_2}{m_1+m_2}+e)u_1+(\frac{m_2(1+e)}{m_1+m_2}-e)u_2} \)

or, \( \displaystyle{v_2=\frac{(1+e)m_1}{m_1+m_2}u_1+\frac{m_2-em_1}{m_1+m_2}u_2}\tag{4} \)

(i) Perfectly inelastic collision:

For perfectly inelastic collision, \( e=0 \)

from equation (3), we get

\( \displaystyle{v_1=\frac{m_1u_1+m_2u_2}{m_1+m_2}} \)

from equation (4), we get

\( \displaystyle{v_2=\frac{m_1u_1+m_2u_2}{m_1+m_2}} \)

So after perfectly inelastic collision the two bodies move with the same velocities. They move as if they were stuck together as a single particle.

(ii) Perfectly elastic collision:

For perfectly elastic collision, \( e=1 \)

from equation (3), we get

\( \displaystyle{v_1=\frac{(m_1-m_2)u_1+2m_2u_2}{m_1+m_2}} \)

from equation (4), we get

\( \displaystyle{v_2=\frac{(m_2-m_1)u_2+2m_1u_1}{m_1+m_2}} \)

So after perfectly elastic collision, the two bodies move with different velocities.