Ans.

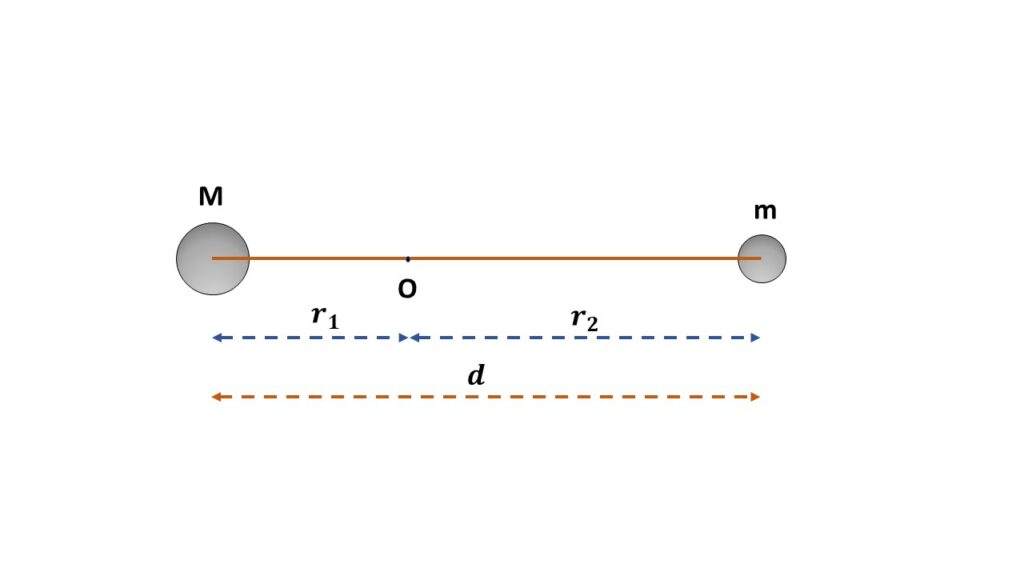
Here the two masses ‘m‘ and ‘M‘ are at a distance d apart.
Let us consider, O be the centre of mass of the system of these two masses, \( r_1 \) be the distance of mass M from the centre of mass O and \( r_2=(d-r_1) \) be the distance of m from the centre of mass O.

So we have, \( Mr_1=mr_2 \)

or, \( Mr_1=m(d-r_1) \)

or, \( Mr_1+mr_1=md \)

or, \( \displaystyle{r_1=\frac{md}{M+m}} \)

Again, \( r_2=d-r_1 \)

or, \( r_2=d-\frac{md}{M+m} \)

or, \( \displaystyle{r_2=\frac{Md}{M+m}} \)

So the moment of inertia of the system through the centre of mass O and perpendicular to the line joining the two masses is

\( I=Mr_1^2+mr_2^2 \)

or, \( I=M{\left(\frac{md}{M+m}\right)}^2+m{\left(\frac{Md}{M+m}\right)}^2 \)

or, \( \displaystyle{I=\frac{Mm^2+mM^2}{{(M+m)}^2}d^2} \)

or, \( \displaystyle{I=\frac{Mm}{M+m}d^2} \)

or, \( \displaystyle{I=\mu{d^2}} \)

Where, \( \mu=\frac{Mm}{M+m} \), is the reduced mass of the system.

Now the rotational kinetic energy of the system is given by,

\( T=\frac{1}{2}I{\omega}^2 \)

or, \( T \) \( =\displaystyle{\frac{1}{2}\mu{d^2}{\omega}^2\\=\frac{1}{2}\frac{Mm}{M+m}d^2(4{\pi}^2{\nu}^2)\\=2{\pi}^2{\nu}^2\frac{Mm}{M+m}d^2} \)

Where, angular velocity \( \omega=2\pi\nu \)