Perpendicular axes theorem (laminar body):
The perpendicular axes theorem states that the sum of moments of inertia of a plane laminar body about any two mutually perpendicular axes in the plane of that laminar body is equal to the moment of inertia of the plane laminar body about a third axis which passes through the intersection of the first two axes, perpendicular to the plane of the lamina.
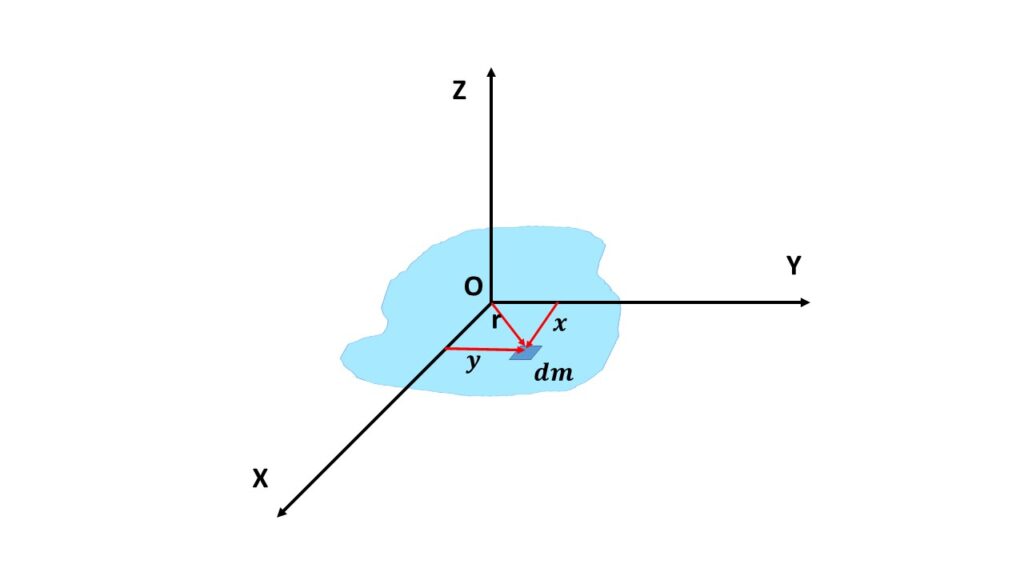
Let us consider a plane laminar body lies in the plane X-Y, let \( I_x \), \( I_y \) and \( I_z \) be the moments of inertia of the body about the X,Y and Z-axes respectively, as shown in Fig.1, then according to the perpendicular axes theorem we can write,
\( I_z=I_x+I_y \).
Proof:
Let us consider an elementary mass of the plane laminar body at a distance r from the origin O, \( x \) and \( y \) be the perpendicular distance from the Y-axis and X-axis respectively. So \( x^2+y^2=r^2 \).
Now, the moment of inertia of the body about the X-axis is \( I_x=\int{y^2}dm \) and the moment o inertia about the Y-axis is \( I_y=\int{x^2}dm \). So the moment of inertia of the body about the Z-axis is
\( I_z=\int{r^2}dm \)
or, \( I_z=\int{x^2+y^2}dm\\=\int{x^2}dm+\int{y^2}dm \)
or, \( I_z=I_x+I_y \)
Perpendicular axes theorem ( 3 dimensioanl body ):
This theorem states that the moments of inertia of a three-dimensional body about any three mutually perpendicular axes is equal to twice the moment of inertia of that body about the point, through which the three mutually perpendicular axes pass.
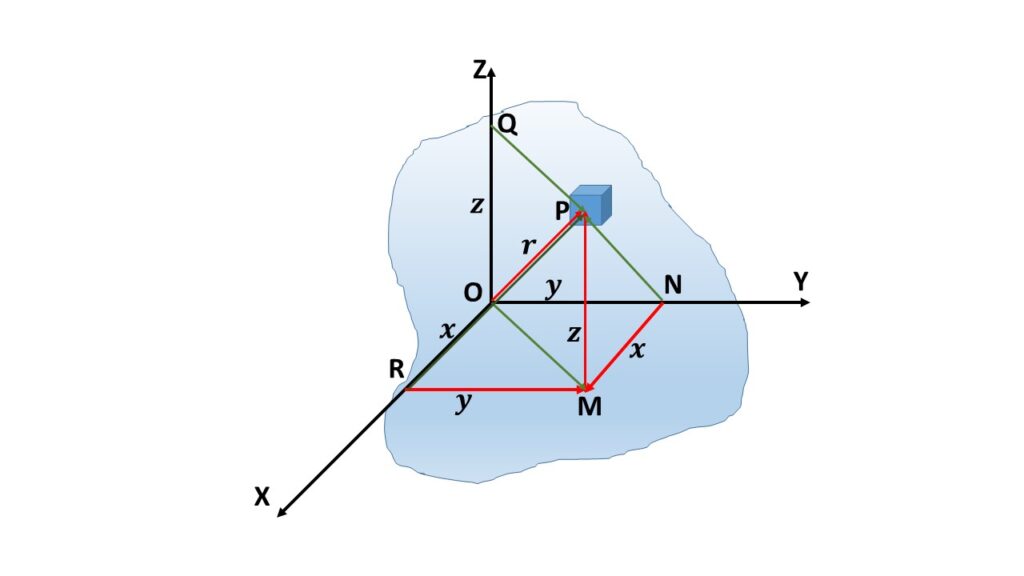
Let us consider \( I_x \), \( I_y \) and \( I_z \) be the moments of inertia of a three-dimensional body about the X-axis, Y-axis and Z-axis respectively, and \( I_r \) be the moment of inertia of the body about the origin. Then according to the theorem of perpendicular axes, we can write \( I_x+I_y+I_z=2I_r \).
Proof:
Let us consider a small element of mass dm at a point P(x.y.z) at a distance \( r \) from the origin \( O \) as shown in Fig.2. PM is perpendicular on the X-Y plane, MR and MN are parallel to the Y-axis and X-axis respectively.
\( r^2= PM^2+MO^2=z^2+(MR^2+RO^2) \)
or, \( r^2==z^2+y^2+x^2 \)
\( I_r=\int{r^2}dm=\int{(x^2+y^2+z^2)}dm \) \( I_x=\int{PR^2}dm\\=\int{(PM^2+MR^2)}dm\\=\int{(z^2+y^2)}dm \) \( I_y=\int{PN^2}dm\\=\int{(PM^2+MN^2)}dm\\=\int{(z^2+x^2)}dm \) \( I_z=\int{PQ^2}dm\\=\int{(MO^2)}dm\\=\int{(MR^2+RO^2)}dm\\=\int{(y^2+x^2)}dm \)Now, \( I_x+I_y+I_z=\int{2(x^2+y^2+z^2)}dm\\=2\int{(x^2+y^2+z^2)}dm\\=2I_r \)