Parallel Axes Theorem:

Parallel axis theorem states that the moment of inertia of a body about any axis is equal to the sum of its moment of inertia about a parallel axis passing through the centre of mass of the body and the product of the mass of that body and the square of the distance between the axes.

\( I=I_0+Ms^2 \), Where
\( I \) is the moment of inertia of the body about any axis,
\( I_0 \) is the moment of inertia of the body about a parallel axis through its centre of mass,
\( M \) is the mass of the body and \( s \) is the distance between the two parallel axes.

Proof:

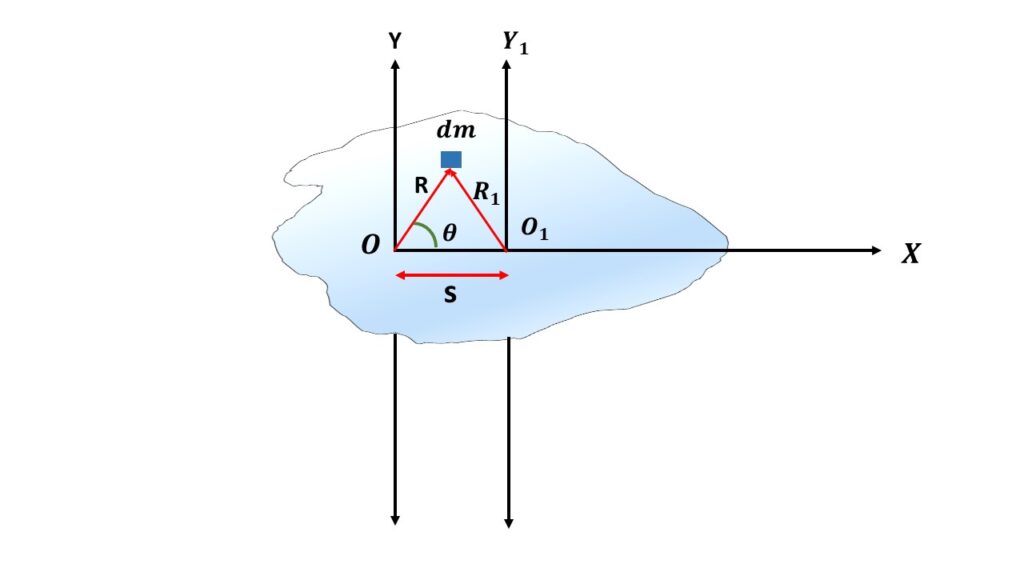
Let us consider two parallel axes, one is OY which passes through the centre of mass of a rigid body and another is \( O_1Y_1 \) which is at a distance s from the axis \( OY \). Let us consider a small mass \( dm \) at a distance \( R \) from the axis \( OY \) and at a distance \( R_1 \) from the axis \( O_1Y_1 \). The total mass of the rigid body is \( M=\int{dm} \).So moment of inertia of the rigid body about the axes \( OY \) and \( O_1Y_ 1 \) are respectively,
\( \displaystyle{I_0=\int{R^2}dm} \) and
\( \displaystyle{I=\int{R_1}^2{dm}} \).
From the above figure we can write,
\( {R_1}^2=R^2+s^2-2sR\cos\theta \)

Now, \( \displaystyle{I=\int{R_1}^2{dm}\\=\int{R^2}dm+\int{s^2}dm-\int{2sR\cos\theta}dm\\=I_0+Ms^2-2s\int{R\cos\theta}dm} \).
Here, \( R\cos\theta \) is the X-coordinate of the mass element with respect to the centre of mass. So \( \displaystyle{\int{R\cos\theta}dm} \) is the moment of mass of the body about the centre of mass axis \( OY \).Since the whole body is balanced about the centre of mass of the body , therefore \( \displaystyle{\int{R\cos\theta}=0} \).

\( \displaystyle{I=I_0+Ms^2} \)