Relation between angular momentum and moment inertia:
Let us consider that a rigid body consists of a large number of particles of masses \( m_1 \), \( m_2 \), \( m_3 \), etc., rotating about a fixed axis \( O_1O_2 \) with a uniform angular velocity \( \omega \). Let \( r_1 \), \( r_2 \), \( r_3 \), etc. be the distances of the masses \( m_1 \), \( m_2 \), \( m_3 \), etc respectively from the axis of rotation. Since the rigid body rotates with a uniform angular velocity, so all the masses also rotate with the same angular velocity. So the linear momentum of the particle of mass \( m_1 \) is \( m_1r_1\omega \).
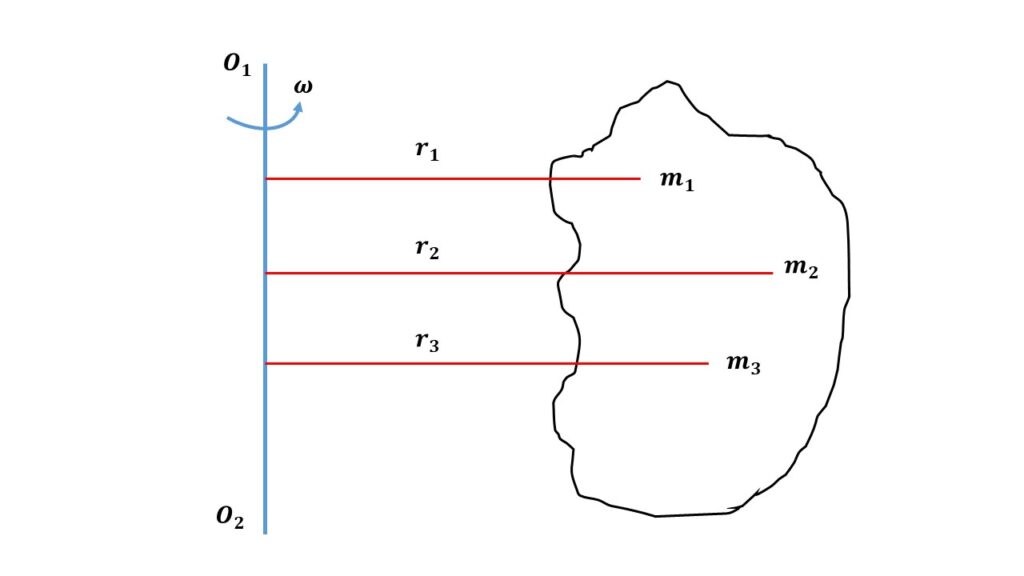
Therefore the moment of momentum of \( m_1 \) about the axis of rotation is \( m_1r_1\omega\times{r_1}=m_1{r_1}^2\omega \). This is also known as angular momentum.
The angular momentum of mass \( m_2 \) about the axis of rotation is \( m_2{r_2}^2\omega \), of mass \( m_3 \) about the axis of rotation is \( m_3{r_3}^2\omega \) and so on.
So the angular momentum of the whole rigid body is given by,
\( L=m_1{r_1}^2\omega+m_2{r_2}^2\omega+m_3{r_3}^2\omega+\cdots\\=(m_1{r_1}^2+m_2{r_2}^2+m_3{r_3}^2+\cdots)\omega\\=(\sum{mr^2})\omega\\=I\omega \)
where, \( I=\sum{mr^2} \) is the moment of inertia of the body about the axis of rotation.