Moment of inertia:

Let us consider, a rigid body is rotating about an fixed axis with a uniform angular velocity \( \omega \). This rigid body consists of a large number of particles of masses \( m_1 \), \( m_2 \), \( m_3 \) etc. and the distance of these particles from the axis of rotation are \( r_1 \), \( r_2 \), \( r_3 \) etc. respectively. Then the rotational kinetic energy of this body is \( E=\frac{1}{2}I{\omega}^2 \),
where \( I=m_1{r_1}^2+m_2{r_2}^2+m_3{r_3}^3+\cdots \)
or, \( I = \sum{mr^2} \) is called the moment of inertia of the body about the axis of rotation.

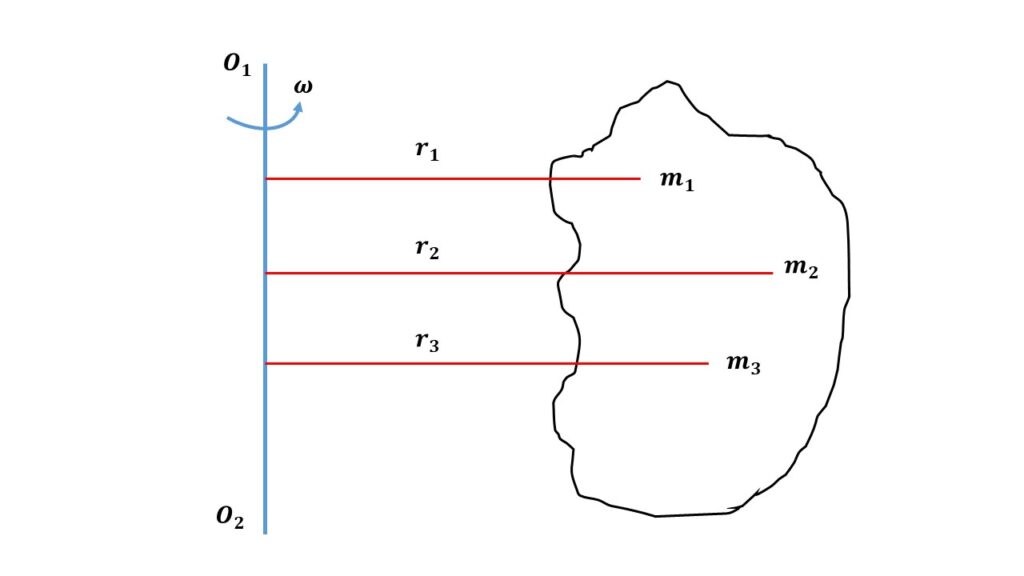
So, the moment of inertia of a body about the axis of rotation is defined by the sum of products of the masses of the particles and the square of the respective distances of the particles from the axis of rotation.

Again, \( E=\frac{1}{2}I{\omega}^2\\or,\ I=\frac{2E}{{\omega}^2} \)
If, \( \omega=1 \) then \( I=2E \).
So the moment of inertia of a body about the axis of rotation is defined as twice the rotational kinetic energy when the angular velocity of the body about that axis of rotation is unity.

In case of continuous mass distribution, let us consider a small element of mass \( dm \) of the rigid body and \( r \) be the distance of that small element from the axis of rotation, then the moment of inertia of the rigid body about that axis of rotation is given by,
\( \displaystyle{I=\int{r^2}dm} \)

Area moment of inertia:

For an area, the moment calculated about any arbitrary axis, say axis-aa is given by,
\( \displaystyle{I_{aa}=\int_{A}{r_{aa}}^2{dA}} \),
where, \( dA \) is a small element on the area A and \( r_{aa} \) is the perpendicular distance between the area \( dA \) and the axis of rotation axis-aa.

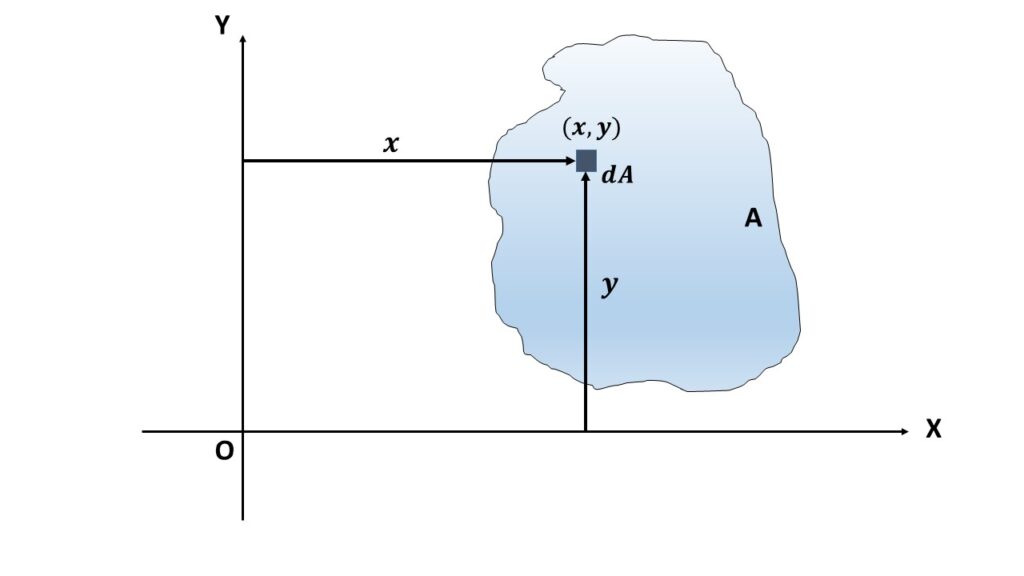
Let’s, put area A in the X-Y rectangular coordinate system. To calculate the moment of inertia of the area with respect to X-axis and Y-axis, let us consider a small differential element of area dA at the location (x,y). Now the perpendicular distance of dA from the Y-axis is \( x \) and the perpendicular distance from the X-axis is \( y \) then,
the moment of inertia about the X-axis is \( \displaystyle{I_X=\int_A{y^2}dA} \) and
the moment of inertia about the Y-axis is \( \displaystyle{I_Y=\int_A{x^2}dA} \).
Just like the area, the area moment of inertia is also positive, and it has the unit of \( [{length}^4] \).

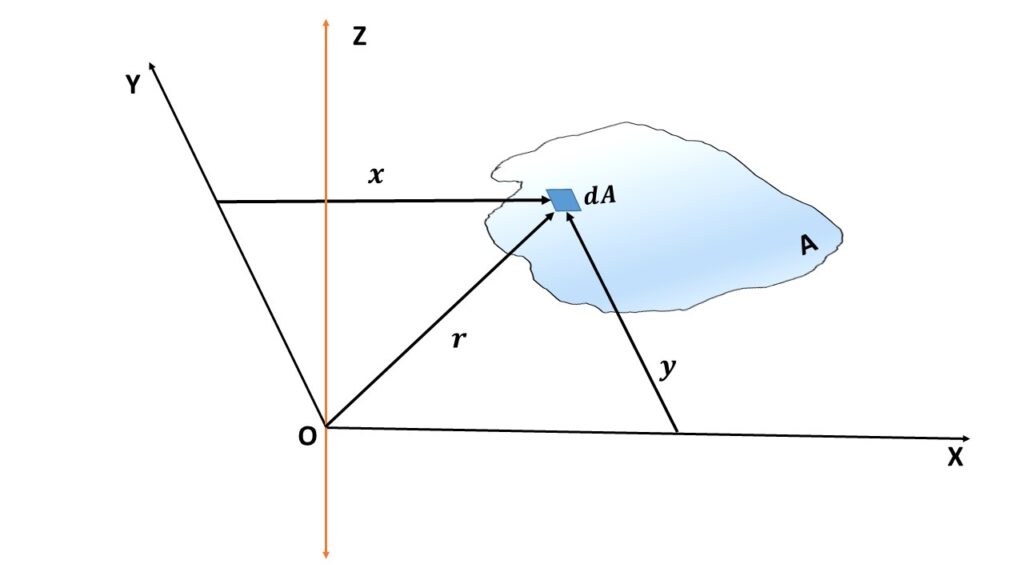
Let’s, find the moment of inertia about the Z-axis which is perpendicular to the X-Y plane and passes through point O. Let \( r \) be the perpendicular distance between the Z-axis and the differential element of area dA. So the moment of inertia of the A about the Z-axis is given by, \( \displaystyle{I_Z=\int_A{r^2}dA} \).

Since the \( x \), \( y \) and \( r \) are the three sides of a right triangle, so according to Pythagorean theorem we can write, \( r=\sqrt{x^2+y^2} \)

Now we can write, \( \displaystyle{I_Z=\int_A{(x^2+y^2)}dA} \)
or, \( \displaystyle{I_Z=I_Y+I_X =I_O\ (say)} \)

In the 2-D representation, \( I_O \) is the polar moment of inertia about the point O, this means actually the area moment of inertia about an axis that is perpendicular to that 2-D plane and passes through the point O.