Depression of the midpoint of a heavy beam supported at two ends and loaded in the middle:
Let, MN represents a uniform rectangular heavy beam of length l and the beam is supported at the ends on the two knife edges, held at the same horizontal plane. Let \( \omega \) be the weight density i.e., weight per unit length of the beam. The beam is loaded with a weight of W at the midpoint O of the beam. So the total weight at the point O is \( W+\omega{l} \), which acts in the vertically downward direction. So the reaction at each knife edge is \( \frac{W+\omega{l}}{2} \) in the vertically upward direction.
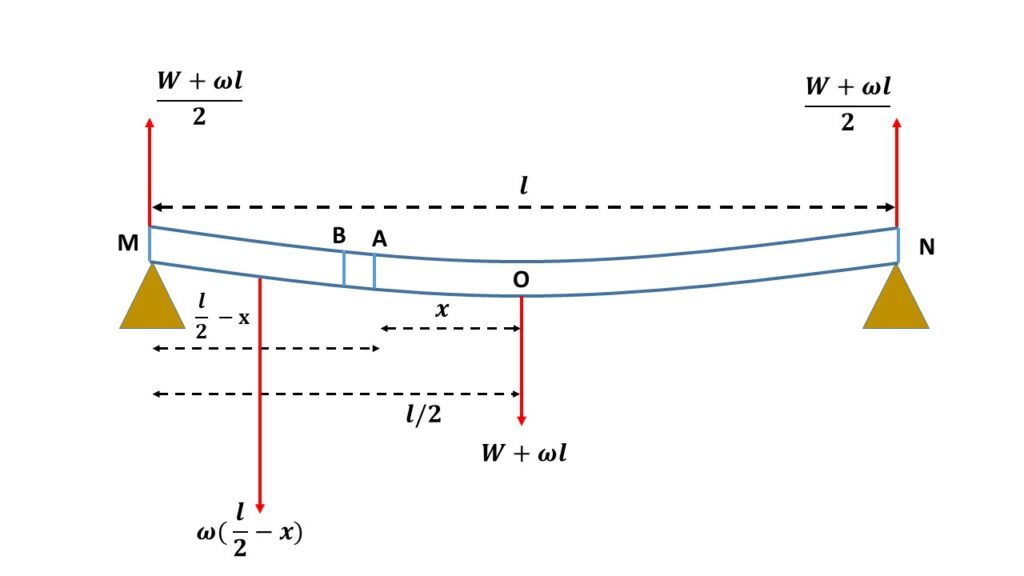
The beam may be considered as equivalent to two inverted cantilevers of length \( \frac{l}{2} \), fixed at the point O, because the middle part of the beam is horizontal.
Let us consider a small portion AB of the beam at a distance \( x \) from the midpoint O of the beam. The weight of the portion ( \( \frac{l}{2}-x \)) of the beam is \( \omega(\frac{l}{2}-x) \), which acts downwards at a distance \( \frac{1}{2}(\frac{l}{2}-x) \) from the section AB.
So the external bending moment about the section AB is
\( \displaystyle{\frac{W+\omega{l}}{2}(\frac{l}{2}-x)-\frac{\omega{(\frac{l}{2}-x)}^2}{2}} \)
Again we know that the internal bending moment is \( \displaystyle{\frac{YI}{R}} \), [Read In Detail] where \( Y \) is Young’s modulus, \( I \) is the geometrical moment of inertia of the beam, \( R \) is the radius of curvature of the neutral axis of \( AB \).
In the equilibrium of the beam, the external bending moment is balanced by the internal bending moment. So
\( \frac{YI}{R}=\frac{W+\omega{l}}{2}(\frac{l}{2}-x)-\frac{\omega{(\frac{l}{2}-x)}^2}{2} \)
or, \( \frac{1}{R}=\frac{1}{YI}[\frac{W+\omega{l}}{2}(\frac{l}{2}-x)-\frac{\omega{(\frac{l}{2}-x)}^2}{2}] \)
or, \( \frac{d\theta}{dx}=\frac{1}{YI}[\frac{W+\omega{l}}{2}(\frac{l}{2}-x)-\frac{\omega{(\frac{l}{2}-x)}^2}{2}] \)
where, \( \frac{1}{R}=\frac{d\theta}{dx} \), \( dx \) is the length of AB and \( d\theta \) is the angle subtended by AB at the centre of curvature.
or, \( d\theta=\frac{W+\omega{l}}{2YI}{(\frac{l}{2}-x)}{dx}-\frac{\omega}{2YI}{(\frac{l}{2}-x)}^2{dx} \)
So the depression of B below A is
\( dy=(\frac{l}{2}-x)d\theta\\=\frac{W+\omega{l}}{2YI}{(\frac{l}{2}-x)}^2{dx}-\frac{\omega}{2YI}{(\frac{l}{2}-x)}^3{dx} \)
So the depression of the midpoint \( O \) of the beam is
\( \displaystyle{y=\frac{W+\omega{l}}{2YI}\int_0^{\frac{l}{2}}{(\frac{l}{2}-x)}^2{dx}\\-\frac{\omega}{2YI}\int_0^{\frac{l}{2}}{(\frac{l}{2}-x)}^3{dx}} \)
\( \displaystyle{\int_0^{\frac{l}{2}}{(\frac{l}{2}-x)}^2{dx}\\=\int_0^{\frac{l}{2}}(\frac{l^2}{4}+x^2-2\frac{l}{2}x)dx\\={[\frac{l^2}{4}x+\frac{x^3}{3}-l\frac{x^2}{2}]}_0^{\frac{l}{2}}\\=(\frac{l^2}{4}\frac{l}{2}+\frac{1}{3}\frac{l^3}{8}-\frac{l}{2}\frac{l^2}{4})\\=l^3(\frac{1}{8}+\frac{1}{24}-\frac{1}{8})\\=\frac{l^3}{24} } \)
\( \displaystyle{\int_0^{\frac{l}{2}}{(\frac{l}{2}-x)}^3{dx}\\=\int_0^{\frac{l}{2}}(\frac{l^3}{8}-3\frac{l^2}{4}x+3\frac{l}{2}x^2-x^3)dx\\=l^4(\frac{1}{16}-\frac{3}{32}+\frac{1}{16}-\frac{1}{64})\\=l^4\frac{1}{64} } \)
\( \displaystyle{y=\frac{W+\omega{l}}{2YI}\frac{l^3}{24}-\frac{\omega{l^4}}{2YI}\frac{1}{64}\\=\frac{Wl^3}{48YI}+\frac{\omega{l^4}}{48YI}-\frac{\omega{l^4}}{128YI}\\=\frac{Wl^3}{48YI}+\frac{\omega{l^4}}{16YI}(\frac{1}{3}-\frac{1}{8})\\=\frac{Wl^3}{48YI}+\frac{5\omega{l^4}}{16YI\times{24}}\\=\frac{Wl^3}{48YI}+\frac{5{W_1}l^3}{384YI}} \)
where, \( W_1=\omega{l} \) is the weight of the beam.