Length of the tube smaller than ‘h’:

The liquid in a capillary tube rises to a maximum height h, given by

\( \displaystyle{T=\frac{r(h+\frac{r}{3})\rho{g}}{2\cos\theta}} \) [ Read In Detail ]

where, r is the radius of the capillary tube, \( \rho \) is the density of the liquid, \( \theta \) is the angle of contact between the liquid and the tube, g is the acceleration due to gravity.

For a fine capillary tube \( r \) is very small and \( \frac{r}{3} \) can be neglected with respect to \( h \). So we get,

\( \displaystyle{T=\frac{rh\rho{g}}{2\cos\theta}} \)

If \( R \) be the radius of the liquid meniscus in the capillary tube, then \( r=R\cos\theta \), where \( r \) is the radius of the capillary tube.

\( \displaystyle{T=\frac{R\cos\theta{hg}\rho}{2\cos\theta}\\=\frac{Rhg\rho}{2}\\or,\ Rh=\frac{2T}{g\rho}\\=constant} \)

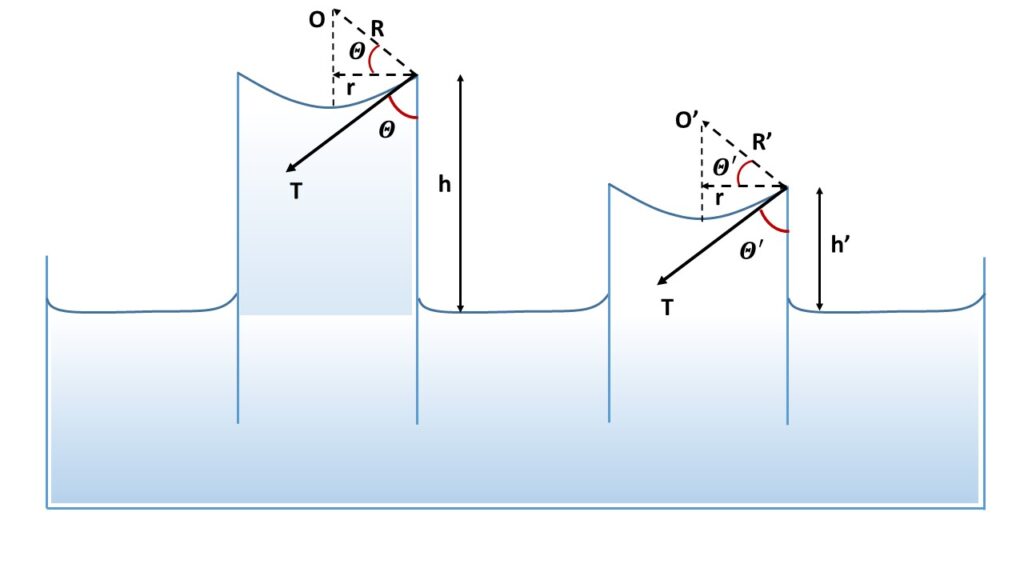
When the length of the capillary tube, say \( h’ \) is less than the maximum height to which the liquid can rise, the liquid will rise to the top of the capillary tube and in its attempt to rise further, the radius of curvature of the liquid surface will increase to a new value \( R’ \) such that \( R’h’=Rh \). this will also cause an increase in the value of angle of contact \( \theta \) because \( r=R\cos\theta \) and the liquid have no tendency to further increase its curvature, where the new angle of contact is \( \theta’ \), such that \( R\cos\theta=R’\cos\theta’=r=constant \).