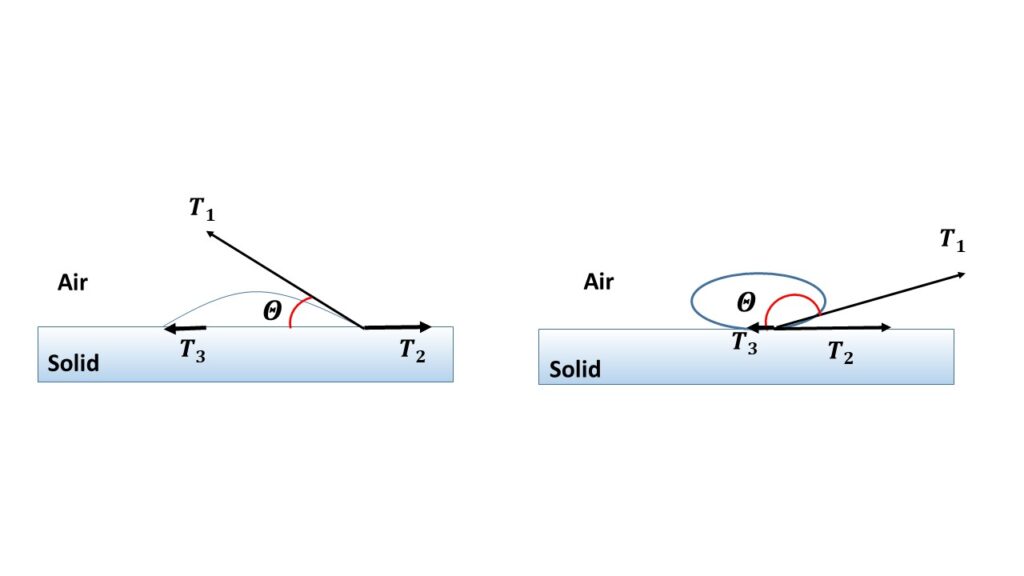
To find whether the angle of contact between a solid and a liquid is obtuse or acute, let us consider the case of a solid, liquid and air in contact. Let θ be the angle of contact and \( T_1 \) be the surface tension of the air-liquid interface, \( T_2 \) be the surface tension of the air-solid interface and \( T_3 \) be the surface tension of the liquid-solid interface respectively as shown in the figure.
In equilibrium,
\( T_3+T_1\cos\theta=T_2\\or,\ \cos\theta=\frac{T_2-T_3}{T_1} \)- If \( T_2>T_3 \), \( \cos\theta \) is positive and \( \theta<90^\circ \) (acute)
- If \( T_2<T_3 \), \( \cos\theta \) is negative and \( \theta>90^\circ \) (obtuse)
- If \( T_2-T_3>T_1 \) or, \( T_2>T_3+T_1 \), \( \cos\theta>1 \) which is positive.
So there will be no equilibrium and the liquid will spread over the solid.