Let us consider a soap bubble is produced from a straw as shown in the adjoining Fig.1, as it moves far the size of the soap bubble increases and ultimately takes a particular size when equilibrium condition is reached. When the soap bubble is grown, the inside pressure of the soap bubble is greater than the outside pressure. Surface tension force has the tendency to decrease the size of the bubble and on the other hand, the inside pressure tends to increase the size of the bubble. At equilibrium condition, these two forces are equal.

Excess pressure:
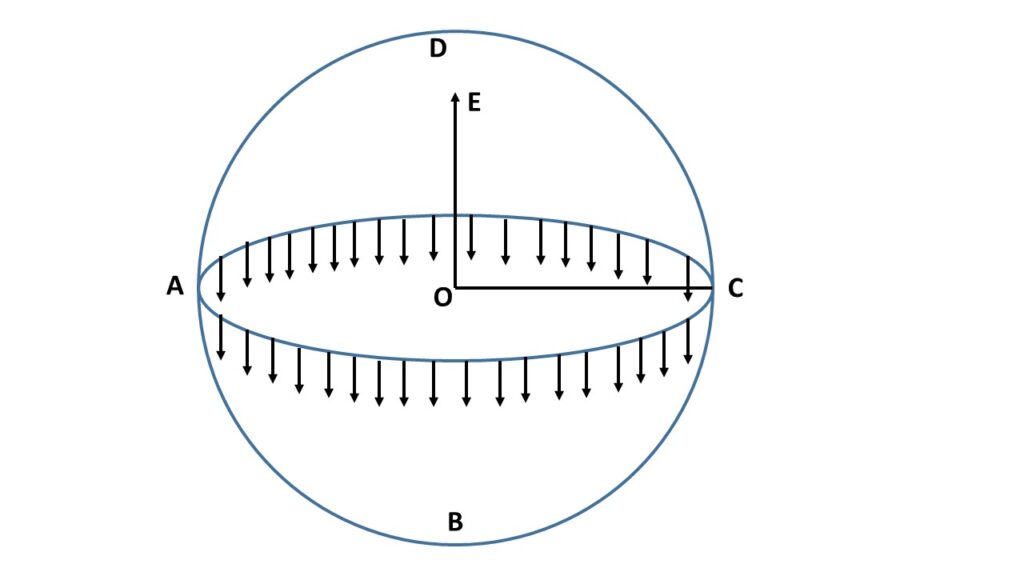
Let us consider a soap bubble \( ABCD \), as shown in the adjoining Fig.2, is in equilibrium condition. This means that the internal pressure of the soap bubble is equal to the external pressure of the soap bubble. Let, with the help of an imaginary place surface \( AC \) through the centre \( O \) of the bubble, the soap bubble \( ABCD \) be divided into two halves. Now the lower half \( ABC \) exerts a push-type force along the direction of \( OE \) on the upper half \( ADC \) due to the excess pressure \( p \) (here excess pressure = internal pressure – surface tensional pressure) so that it moves in outward direction \( OE \) and the size of \( ADC \) increases and the force arising due to excess pressure is \( p\times\pi{r}^2 \), where \( r \) is the radius of the bubble.
On the other hand, \( ABC \) tends to exert a pull-type force \( 2T\times{2\pi{r}} \) on the upper half \( ADC \) due to surface tension so that it may not go out, where \( T \) is the surface tension of the liquid. Under isothermal condition, there is only surface tensional force. For equilibrium of the soap bubble,
\( p\times{\pi{r}^2}=2T\times{2\pi{r}} \)or, \( \displaystyle{p=\frac{4T}{r}} \).
This is the equation of excess pressure inside a soap bubble.